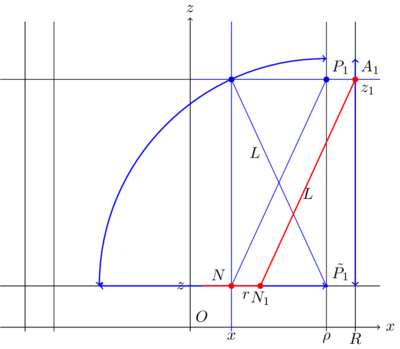Difference between revisions of "Projets:Perso:2014:Robot Delta"

From Electrolab
Jump to: navigation, search
(synchro avec erreur tex)
(update)
Line 247: Line 247:
 
</math>
 
</math>
  
−
On réécrit le systèmes d'équations en introduisant les cordonnées <math>q_i</math> comme cela:
+
== Matrice Jacobienne ==
  
−
<math> L^2 - (z - z_i)^2 = q_i = (x - x_i)^2 + (y - y_i)^2 </math>
+
En dérivant le système d'équations par rapport au temps, on obtiens le système d'équations différentielles suivant :
  
−
avec <math> z_i = z^2 - \sqrt{L^2 - q_i^2} </math>
+
<math>
 +
\Delta z_i\dot{z_i} = \Delta x_i\dot{x} + \Delta y_i\dot{y} + \Delta z_i\dot{z}
 +
</math>
  
−
En calcul variationnel, on obtient
+
où <math> \Delta X_i = X - X_i </math>
 +
 
 +
qui se réécrit sous forme matricielle :
 +
 
 +
<math> \dot{Z} = J \dot{P} </math>
 +
 
 +
où <math> \dot{P} = \begin{pmatrix} \dot{x} \\ \dot{y} \\ \dot{z} \end{pmatrix} </math> et
 +
<math> \dot{Z} = \begin{pmatrix} \dot{z_1} \\ \dot{z_2} \\ \dot{z_3} \end{pmatrix} </math>
 +
 
 +
La matrice Jacobienne <math>J</math> (ou Jacobien) s'écrit alors :
 +
 
 +
<math>
 +
J = \begin{pmatrix}
 +
\frac{\Delta x_1}{\Delta z_1} & \frac{\Delta y_1}{\Delta z_1} & 1 \\
 +
\frac{\Delta x_2}{\Delta z_2} & \frac{\Delta y_2}{\Delta z_2} & 1 \\
 +
\frac{\Delta x_3}{\Delta z_3} & \frac{\Delta y_3}{\Delta z_3} & 1 \\
 +
\end{pmatrix}
 +
</math>
 +
 
 +
Le Jacobien permet de calculer la vitesse des coulisseaux en fonction de la vitesse de la nacelle.
 +
 
 +
Les points singuliers peuvent être déterminé à partir du déterminant du Jacobien :
 +
 
 +
<math>
 +
det(J) = \frac{\eta}{\Delta z_1\,\Delta z_2\,\Delta z_3}
 +
</math>
 +
 
 +
où
 +
<math>
 +
\eta = (\Delta x_1\,\Delta y_2 - \Delta x_2\,\Delta y_1)\Delta z_3 + (\Delta x_3\,\Delta y_1 - \Delta x_1\,\Delta y_3)\Delta z_2 + (\Delta x_2\,\Delta y_3 - \Delta x_3\,\Delta y_2)\Delta z_1
 +
</math>
 +
 
 +
L'inverse du Jacobien s'écrit:
 +
 
 +
<math>
 +
J^{-1} =
 +
\frac{1}{\eta}
 +
\begin{pmatrix}
 +
  \Delta y_2\,\Delta z_1\,\Delta z_3 - \Delta y_3\,\Delta z_1\,\Delta z_2 &
 +
-\Delta y_1\,\Delta z_2\,\Delta z_3 + \Delta y_3\,\Delta z_1\,\Delta z_2 &
 +
  \Delta y_1\,\Delta z_2\,\Delta z_3 - \Delta y_2\,\Delta z_1\,\Delta z_3 \\
 +
-\Delta x_2\,\Delta z_1\,\Delta z_3 + \Delta x_3\,\Delta z_1\,\Delta z_2 &
 +
  \Delta x_1\,\Delta z_2\,\Delta z_3 - \Delta x_3\,\Delta z_1\,\Delta z_2 &
 +
-\Delta x_1\,\Delta z_2\,\Delta z_3 + \Delta x_2\,\Delta z_1\,\Delta z_3 \\
 +
  (\Delta x_2\,\Delta y_3 - \Delta x_3\,\Delta y_2)\Delta z_1 &
 +
-(\Delta x_1\,\Delta y_3 - \Delta x_3\,\Delta y_1)\Delta z_2 &
 +
(\Delta x_1\,\Delta y_2 - \Delta x_2\,\Delta y_1)\Delta z_3 \\
 +
\end{pmatrix}
 +
</math>
  
−
<math> d z_i = - \frac{q_i}{\sqrt{L^2 - q_i^2}} d q_i </math>
+
Le système est non singulier si et seulement si le déterminant ou de manière équivalente <math>\eta</math> est différent de zéro.
  
 
== Cinématique directe ==
 
== Cinématique directe ==
Line 323: Line 373:
 
Afin d'exprimer les coordonnées de la solution dans le référentiel d'origine, nous allons exprimer le changement de repère:
 
Afin d'exprimer les coordonnées de la solution dans le référentiel d'origine, nous allons exprimer le changement de repère:
  
−
<math> P = P1 + x\;\hat{e}_x + y\;\hat{e}_y + z\;\hat{e}_z </math>
+
<math> P = P_1 + x\;\hat{e}_x + y\;\hat{e}_y + z\;\hat{e}_z </math>
  
 
Le premier vecteur unitaire s'écrit:
 
Le premier vecteur unitaire s'écrit:
  
−
<math> \hat{e}_x = \frac{P2 - P1}{\| P2 - P1 \|} </math>
+
<math> \hat{e}_x = \frac{P_2 - P_1}{\| P_2 - P_1 \|} </math>
  
 
et les deux premières distances:
 
et les deux premières distances:
Line 333: Line 383:
 
<math>
 
<math>
 
\begin{align}
 
\begin{align}
−
   d &= \| P2 - P1 \| \\
+
   d &= \| P_2 - P_1 \| \\
−
   i &= (P3 - P1)  \cdot \hat{e}_x
+
   i &= (P_3 - P_1)  \cdot \hat{e}_x
 
\end{align}
 
\end{align}
 
</math>
 
</math>
Line 340: Line 390:
 
Le second vecteur unitaire s'écrit:
 
Le second vecteur unitaire s'écrit:
  
−
<math> \hat{e}_y = \frac{P3 - P1 - i\;\hat{e}_x}{\| P3 - P1 - i\;\hat{e}_x \|} </math>
+
<math> \hat{e}_y = \frac{P_3 - P_1 - i\;\hat{e}_x}{\| P_3 - P_1 - i\;\hat{e}_x \|} </math>
  
 
et la troisième distance:
 
et la troisième distance:
  
−
<math> j = ( P3 - P1 ) \cdot \hat{e}_y </math>
+
<math> j = ( P_3 - P_1 ) \cdot \hat{e}_y </math>
  
 
Le troisième vecteur unitaire s'écrit <math> \hat{e}_z = \hat{e}_x \times \hat{e}_y </math>
 
Le troisième vecteur unitaire s'écrit <math> \hat{e}_z = \hat{e}_x \times \hat{e}_y </math>
  
 
Nous avons à présent résolut la cinématique directe de manière analytique, mais il n'existe pas d'expression simple de la position de la nacelle en fonction des positions des bras. C'est pourquoi nous ne chercherons pas à développer les expressions.
 
Nous avons à présent résolut la cinématique directe de manière analytique, mais il n'existe pas d'expression simple de la position de la nacelle en fonction des positions des bras. C'est pourquoi nous ne chercherons pas à développer les expressions.
 +
 +
On définit <math> z_{ij} = z_i - z_j </math>.
 +
 +
<math>
 +
  \mathcal{P}_{21} = \begin{pmatrix} -\frac{3}{2}\rho \\  \frac{\sqrt{3}}{2}\rho \\ z_{21} \end{pmatrix} \quad
 +
  \mathcal{P}_{31} = \begin{pmatrix} -\frac{3}{2}\rho \\ -\frac{\sqrt{3}}{2}\rho \\ z_{31} \end{pmatrix} \quad
 +
  \mathcal{P}_{32} = \begin{pmatrix} 0 \\ -\sqrt{3}\rho \\ z_{32} \end{pmatrix}
 +
</math>
 +
 +
<math>
 +
  \mathcal{L}_{21} = \sqrt{3\rho^2 + z_{21}^2} \quad
 +
  \mathcal{L}_{31} = \sqrt{3\rho^2 + z_{31}^2} \quad
 +
  \mathcal{L}_{32} = \sqrt{3\rho^2 + z_{32}^2}
 +
</math>
 +
 +
<math>
 +
  x\;\hat{e}_x = \frac{\mathcal{P}_{21}}{2} =
 +
  \begin{pmatrix} -\frac{3}{4}\rho \\ \frac{\sqrt{3}}{4}\rho \\ \frac{z_{21}}{2} \end{pmatrix}
 +
</math>
 +
 +
<math>
 +
  i = \frac{\mathcal{P}_{31} . \mathcal{P}_{21}}{d} = \frac{1}{d} \left( \frac{3}{2}\rho^2 + z_{21}z_{31} \right)
 +
</math>
 +
 +
<math>
 +
i^2 + j^2 = \mathcal{L}_{31}^2 = 3\rho^2 + z_{31}^2
 +
</math>
 +
 +
<math>
 +
  y = \frac{\mathcal{L}_{31}^2 - \mathcal{P}_{31}\mathcal{P}_{21}}{2 \mathcal{P}_{31} . \hat{e}_y}
 +
    = \frac{\frac{3}{2}\rho^2 + z_{31}^2 - z_{21}z_{31}}{2 \mathcal{P}_{31} . \hat{e}_y}
 +
</math>
 +
 +
<math>
 +
  i . \hat{e}_x = \mathcal{P}_{31} . \mathcal{P}_{21} \frac{\mathcal{P}_{21}}{d}
 +
</math>
  
 
== Cinématique dans un plan z ==
 
== Cinématique dans un plan z ==

Revision as of 16:45, 4 May 2014

Robot Delta
Auteur Fabrice
Tags du projet robot, imprimante 3d, delta
Utilisateur final ceux qui aiment la cinématique et la théorie des groupes
Type de projet

Projet personnel de Fabrice

Projet Robot Delta

Cette page a pour vocation de rassembler des informations sur les robots Delta.




Todo

  • trier les références
  • calculer l'espace de travail
  • calculer l'amplitude angulaire des rotules
  • ajouter une étude statique et dynamique
  • étude variationnelle pour évaluer la précision

Liens Externes

  • Ce dépôt GitHub contient les fichiers annexes: git@github.com:FabriceSalvaire/linear-delta-robot.git

Les Robots Delta

Le robot Delta a été inventé par Reymond Clavel en 1985, ingénieur doctorant à l'École polytechnique fédérale de Lausanne (EPFL), afin de répondre à la problématique d'un robot manipulateur doté de trois degrés de liberté et une grande accélération. En l’occurrence la première implémentation fût un robot manipulateur de chocolats.

Par rapport aux architectures classiques tel que le robot Scara (Selective Compliance Assembly Robot Arm), les robots delta peuvent atteindre de très grandes accélérations mais avec un volume de travail plus restreint et une cinématique bien plus complexe qu'un centre d'usinage 3 axes classique.

L'architecture est particulièrement adapté à des mouvements rapides dans l'espace et des efforts sur l'axe Z du robot.

Le Robot Delta Linéaire (Vertical)

La nacelle a 3 degrés de liberté qui sont les trois translations dans l'espace. Elle reste toujours parallèle au plan horizontale, contrairement à une plateforme de Stewart (hexapod) qui peut faire varier la longueur de ses 6 bras et faire tourner la nacelle. La position de la nacelle est entièrement déterminé par les positions verticales des articulations hautes des trois bras.

Rostock-animation.gif

Exemples de réalisations

Exemples de réalisations dans l'industrie

  • Urane SX de Comau (ex RENAULT AUTOMATION de Castres) et développé à l'origine par le LIRMM (Laboratoire d'informatique, de robotique et de micro-électronique CNRS-Université Montpellier 2). Ce centre d’usinage horizontal est basé sur une architecture Delta linéaire et des moteurs linéaires, ce qui la rend particulièrement adapté à l'usinage grande vitesse de trous, alésages et lamages.

Exemples de réalisations d'imprimantes 3D

Exemples de réalisations de CNCs

Une delta linéaire verticale piloté par EMC2:


Une delta linéaire horizontale:


Une plateforme de Stewart (Hexapod) avec une petite tête de fraisage, piloté par EMC2:

  • vidéo 1
  • vidéo 2
  • réalisation plutôt sérieuse
  • 3*2 bras montés sur vis à bille et joint de cardan (mais pas de détail sur la mécanique)


Design intéressant d'une delta classique légère:

  • vidéo
  • moteur d’essuie glace avec encodeur magnétique et électronique ad hoc
  • conception légère mais suffisante pour une imprimante 3D (à vérifier)

Bibliographie

Tous les PDF sont disponible via Google ...

Raymond Clavel, le père du robot Delta

Livres

  • A mathematical introduction to robotic manipulation, Richard M. Murray, California Institute of Technology, Zexiang Li, Hong Kong University of Science and Technology, S. Shankar Sastry, University of California, Berkeley, CRC Press, http://www.cds.caltech.edu/~murray/mlswiki
  • Parallel Robots, J.-P. MERLET, INRIA, Sophia-Antipolis, Springer
  • Robot Manipulator Control Theory and Practice, Frank L.Lewis, University of Texas, Darren M.Dawson, University Clemson, Chaouki T.Abdallah, University of New Mexico, Marcel Dekker

Thèses

  • Analyse cinétostatique des machines parallèles à translations, thèse de Félix MAJOU, École Centrale Nantes
  • Analysis and Synthesis of Parallel Robots for Medical Applications, thesis of Nabil Simaan, Technion, Israel Institute Of Technology
  • Conception de robots de très haute précision à articulations flexibles: interaction dynamique-commande, thèse de Jean-Philippe BACHER, EPFL
  • Contribution à l’amélioration de la précision des robots parallèles, thèse de David Corbel, université Montpellier II
  • Design and Analysis of a Three Degrees of Freedom Parallel Kinematic Machine, thesis of Xiaolin Hu, University of Ontario Institute of Technology
  • Improving the accuracy of parallel robots, Thesis of Peter Vischer, EPFL

Articles

  • A New Approach to the Design with a Desired Workspace of a DELTA Robot, Xin-Jun Liu et al., Journal of Intelligent and Robotic Systems 39: 209–225, 2004
  • Advanced Synthesis of the DELTA Parallel Robot for a Specified Workspace, M.A. Laribi et al.
  • Approche multicritère pour la conception optimale des robots parallèles en considérant les performances cinématiques et élastostatiques, A. BELLOULA et al., 21ème Congrès Français de Mécanique
  • Argos: A Novel 3-DoF Parallel Wrist Mechanism, Peter Vischer and Reymond Clavel, The International Journal of Robotics Research 2000; 19; 5, DOI: 10.1177/02783640022066707
  • Dynamic analysis of clavel’s delta parallel robot, Staicu St., Carp-Ciocardia D. C., Proceedings of the 2003 IEEE International Conference on Robotics & Automation Taipei, Taiwan, September 14-19, 2003
  • Kinematic analysis of a 3-PRS parallel manipulator, Yangmin Li , Qingsong Xu, Robotics and Computer-Integrated Manufacturing 23 (2007) 395–408
  • Mobilité dans les chaînes cinématiques, application à la conception structurale des robots manipulateurs, Jacques M. HERVÉ, ECP
  • Performance analysis of 3 DOF Delta parallel robot, Sergiu-Dan Stan et al., HSI 2011
  • Robots for high speed manipulation, Viera Poppeová et al., ISSN 1330-3651, UDC/UDK 681.51:004.896
  • Workspace computation in parallel manipulators with three translational degrees of freedom, Giovanni Boschetti, Roberto Caracciolo

Cinématique d'un robot delta linéaire vertical

Symétries

Le robot delta linéaire verticale est invariant par translation (positive) selon l'axe vertical et invariant par rotation de 2 ⁢ π 3 2 𝜋 3 selon ce même axe. Les trois axes verticaux forment un triangle équilatéral et sont inscrit dans un cercle centré à l'origine du référentiel.

Pièces et liaisons cinématiques

Pièces:

  • 3 glissières/hélicoïdales formant le châssis
  • 3 bras reliant la nacelle aux glissières
  • une nacelle

Configuration verticale avec rotule:

  • liaison glissière/hélicoïdale verticale
  • liaison rotule à chaque extrémité du double bras (un ressort placé entre le double bras limite la rotation des bras)

Configuration verticale avec joint de cardan:

  • liaison glissière/hélicoïdale verticale
  • liaison rotule à doigt (cardan) à chaque extrémité du bras

Géométrie du robot

Schema-top-view.png
Schema-side-view.png
Schema-top-view-moved.png
Schema-top-view-moved-sphere.png

Glissement progressif vers le plaisir ... cinématique!

L'ensemble des calculs ont été vérifié ou calculé avec l'antique logiciel de calcul formel Maxima qui est Open Source (libéré en octobre 1998 sous l'impulsion de William Schelter et l'accord du DOE). lien vers le fichier linear-delta-robot.mac.

Colophon: Les figures ont été réalisé avec l'époustouflant package Tikz pour LaTeX développé par Till Tantau qui permet de faire des graphiques complexes et de qualité irréprochable. Un exemple en matière de conception logiciel où il est difficile de trouver les limites, bien que TeX est été conçu en 1977.

Le référentiel de la machine à pour origine O 𝑂 le centre de symétrie du plateau bas, l'axe des x 𝑥 pointe vers un des trois axes verticaux et l'axe des z 𝑧 pointe vers le haut. Le référentiel forme un trièdre direct, ce qui défini l'axe des y 𝑦 .

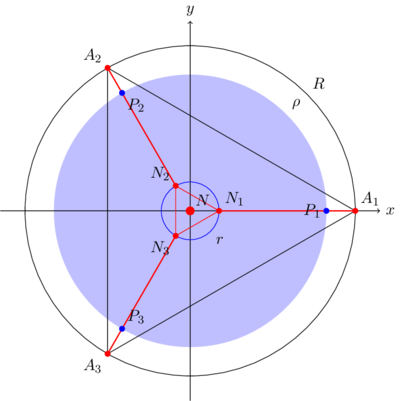
Les centres des rotules au niveau des trois axes verticaux sont notés A i subscript 𝐴 𝑖 où i = 1 , 2 , 3 𝑖 1 2 3 et sont disposés de manière équidistante sur un cercle de centre R 𝑅 aux angles θ i = 2 ⁢ π 3 ⁢ ( i - 1 ) subscript 𝜃 𝑖 2 𝜋 3 𝑖 1 et à la position z i subscript 𝑧 𝑖 sur l'axe vertical.

On note ℛ i = ( c ⁢ o ⁢ s ⁢ ( θ i ) - s ⁢ i ⁢ n ⁢ ( θ i ) s ⁢ i ⁢ n ⁢ ( θ i ) c ⁢ o ⁢ s ⁢ ( θ i ) ) subscript ℛ 𝑖 𝑐 𝑜 𝑠 subscript 𝜃 𝑖 𝑠 𝑖 𝑛 subscript 𝜃 𝑖 𝑠 𝑖 𝑛 subscript 𝜃 𝑖 𝑐 𝑜 𝑠 subscript 𝜃 𝑖 la rotation d'angle θ i subscript 𝜃 𝑖 .

Les rotations correspondantes aux trois axes sont:

ℛ 1 = I 2   ℛ 2 = - 1 2 ⁢ ( 1 3 - 3 1 )   ℛ 3 = - 1 2 ⁢ ( 1 - 3 3 1 ) formulae-sequence subscript ℛ 1 subscript 𝐼 2 formulae-sequence subscript ℛ 2 1 2 1 3 3 1 subscript ℛ 3 1 2 1 3 3 1

Le centre de la nacelle est notée N = ( x y z ) 𝑁 𝑥 𝑦 𝑧 et les centres des rotules sont notés N i subscript 𝑁 𝑖 et sont disposés sur un cercle de centre r 𝑟 et aux angles θ i subscript 𝜃 𝑖 .

Les bras ont une longueur constante L = ∥ A i ⁢ N i → ∥ 𝐿 norm → subscript 𝐴 𝑖 subscript 𝑁 𝑖 . On note ρ = R - r 𝜌 𝑅 𝑟 la longueur minimal des bras pour lequel la nacelle est connecté mais figé au centre. Usuellement on choisira une longueur plus grande afin d'avoir une amplitude de mouvement suffisante. La nacelle sera toujours en dessous des articulations par construction. Le rayon ρ 𝜌 corresponds aussi à la limite au delà duquel la nacelle peut heurté les axes verticaux, on considère par la suite que l'espace de travail est nécessairement inclue dans ce cercle.

La position de la nacelle est entièrement déterminé par les coordonnées z i subscript 𝑧 𝑖 .

Cinématique indirecte

On résout la cinématique indirecte en fermant la chaîne cinématique pour chaque bras:

A i ⁢ N i → = O ⁢ N → + N ⁢ N i → - O ⁢ A i → → subscript 𝐴 𝑖 subscript 𝑁 𝑖 → 𝑂 𝑁 → 𝑁 subscript 𝑁 𝑖 → 𝑂 subscript 𝐴 𝑖 . On définit les points P i = ( x i y i z i ) subscript 𝑃 𝑖 subscript 𝑥 𝑖 subscript 𝑦 𝑖 subscript 𝑧 𝑖 où ( x i y i ) = ℛ i ⁢ ( ρ 0 ) subscript 𝑥 𝑖 subscript 𝑦 𝑖 subscript ℛ 𝑖 𝜌 0 qui sont les points homothétiques des points A i subscript 𝐴 𝑖 sur le cercle de rayon ρ 𝜌 . Les coordonnées des points P i subscript 𝑃 𝑖 s'écrivent: 𝒫 1 = ρ ⁢ ( 1 0 z 1 )   𝒫 2 = ρ 2 ⁢ ( - 1 3 z 2 )   𝒫 3 = - ρ 2 ⁢ ( 1 3 z 3 ) formulae-sequence subscript 𝒫 1 𝜌 1 0 subscript 𝑧 1 formulae-sequence subscript 𝒫 2 𝜌 2 1 3 subscript 𝑧 2 subscript 𝒫 3 𝜌 2 1 3 subscript 𝑧 3

Il vient A i ⁢ N i → = N - P i → subscript 𝐴 𝑖 subscript 𝑁 𝑖 𝑁 subscript 𝑃 𝑖 .

À partir de la norme de ce vecteur, on obtient un système de 3 équations reliant les coordonnées z i subscript 𝑧 𝑖 et la position de la nacelle:

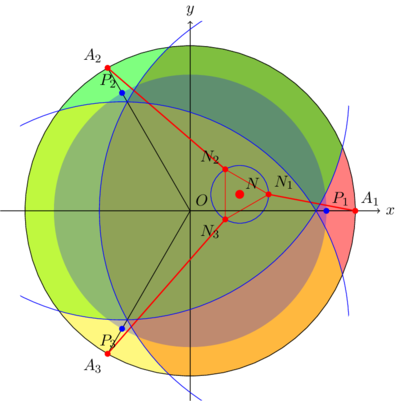
L 2 = ( x - x i ) 2 + ( y - y i ) 2 + ( z - z i ) 2 superscript 𝐿 2 superscript 𝑥 subscript 𝑥 𝑖 2 superscript 𝑦 subscript 𝑦 𝑖 2 superscript 𝑧 subscript 𝑧 𝑖 2 Chaque équation représente une sphère de rayon L 𝐿 centré sur le projeté du point P i subscript 𝑃 𝑖 sur le plan de la nacelle. On choisit ce point car il permet de déterminer z i subscript 𝑧 𝑖 . On tire du système d'équations la relation de la cinématique indirecte: z i = z + L 2 - ( x - x i ) 2 - ( y - y i ) 2 subscript 𝑧 𝑖 𝑧 superscript 𝐿 2 superscript 𝑥 subscript 𝑥 𝑖 2 superscript 𝑦 subscript 𝑦 𝑖 2 puisque z < z i 𝑧 subscript 𝑧 𝑖 par construction. On en déduit la contrainte géométrique ( x - x i ) 2 + ( y - y i ) 2 < L 2 superscript 𝑥 subscript 𝑥 𝑖 2 superscript 𝑦 subscript 𝑦 𝑖 2 superscript 𝐿 2 , le centre de la nacelle est inscrit dans un cercle de rayon L 𝐿 centré sur le point P i subscript 𝑃 𝑖 . L'intersection de ces trois cercles forment l'espace de travail de la machine. Le système d'équations s'écrit en exprimant les points P i subscript 𝑃 𝑖 : L 2 = ( x - ρ ) 2 + y 2 + ( z - z 1 ) 2 L 2 = ( x + ρ 2 ) 2 + ( y + 3 2 ⁢ ρ ) 2 + ( z - z 2 ) 2 L 2 = ( x + ρ 2 ) 2 + ( y - 3 2 ⁢ ρ ) 2 + ( z - z 3 ) 2 superscript 𝐿 2 absent superscript 𝑥 𝜌 2 superscript 𝑦 2 superscript 𝑧 subscript 𝑧 1 2 superscript 𝐿 2 absent superscript 𝑥 𝜌 2 2 superscript 𝑦 3 2 𝜌 2 superscript 𝑧 subscript 𝑧 2 2 superscript 𝐿 2 absent superscript 𝑥 𝜌 2 2 superscript 𝑦 3 2 𝜌 2 superscript 𝑧 subscript 𝑧 3 2

Matrice Jacobienne

En dérivant le système d'équations par rapport au temps, on obtiens le système d'équations différentielles suivant :

Δ ⁢ z i ⁢ z i ˙ = Δ ⁢ x i ⁢ x ˙ + Δ ⁢ y i ⁢ y ˙ + Δ ⁢ z i ⁢ z ˙ Δ subscript 𝑧 𝑖 ˙ subscript 𝑧 𝑖 Δ subscript 𝑥 𝑖 ˙ 𝑥 Δ subscript 𝑦 𝑖 ˙ 𝑦 Δ subscript 𝑧 𝑖 ˙ 𝑧 où Δ ⁢ X i = X - X i Δ subscript 𝑋 𝑖 𝑋 subscript 𝑋 𝑖 qui se réécrit sous forme matricielle : Z ˙ = J ⁢ P ˙ ˙ 𝑍 𝐽 ˙ 𝑃 où P ˙ = ( x ˙ y ˙ z ˙ ) ˙ 𝑃 ˙ 𝑥 ˙ 𝑦 ˙ 𝑧 et Z ˙ = ( z 1 ˙ z 2 ˙ z 3 ˙ ) ˙ 𝑍 ˙ subscript 𝑧 1 ˙ subscript 𝑧 2 ˙ subscript 𝑧 3 La matrice Jacobienne J 𝐽 (ou Jacobien) s'écrit alors : J = ( Δ ⁢ x 1 Δ ⁢ z 1 Δ ⁢ y 1 Δ ⁢ z 1 1 Δ ⁢ x 2 Δ ⁢ z 2 Δ ⁢ y 2 Δ ⁢ z 2 1 Δ ⁢ x 3 Δ ⁢ z 3 Δ ⁢ y 3 Δ ⁢ z 3 1 ) 𝐽 Δ subscript 𝑥 1 Δ subscript 𝑧 1 Δ subscript 𝑦 1 Δ subscript 𝑧 1 1 Δ subscript 𝑥 2 Δ subscript 𝑧 2 Δ subscript 𝑦 2 Δ subscript 𝑧 2 1 Δ subscript 𝑥 3 Δ subscript 𝑧 3 Δ subscript 𝑦 3 Δ subscript 𝑧 3 1

Le Jacobien permet de calculer la vitesse des coulisseaux en fonction de la vitesse de la nacelle.

Les points singuliers peuvent être déterminé à partir du déterminant du Jacobien :

d ⁢ e ⁢ t ⁢ ( J ) = η Δ ⁢ z 1 ⁢ Δ ⁢ z 2 ⁢ Δ ⁢ z 3 𝑑 𝑒 𝑡 𝐽 𝜂 Δ subscript 𝑧 1 Δ subscript 𝑧 2 Δ subscript 𝑧 3

où

η = ( Δ ⁢ x 1 ⁢ Δ ⁢ y 2 - Δ ⁢ x 2 ⁢ Δ ⁢ y 1 ) ⁢ Δ ⁢ z 3 + ( Δ ⁢ x 3 ⁢ Δ ⁢ y 1 - Δ ⁢ x 1 ⁢ Δ ⁢ y 3 ) ⁢ Δ ⁢ z 2 + ( Δ ⁢ x 2 ⁢ Δ ⁢ y 3 - Δ ⁢ x 3 ⁢ Δ ⁢ y 2 ) ⁢ Δ ⁢ z 1 𝜂 Δ subscript 𝑥 1 Δ subscript 𝑦 2 Δ subscript 𝑥 2 Δ subscript 𝑦 1 Δ subscript 𝑧 3 Δ subscript 𝑥 3 Δ subscript 𝑦 1 Δ subscript 𝑥 1 Δ subscript 𝑦 3 Δ subscript 𝑧 2 Δ subscript 𝑥 2 Δ subscript 𝑦 3 Δ subscript 𝑥 3 Δ subscript 𝑦 2 Δ subscript 𝑧 1 L'inverse du Jacobien s'écrit: Failed to parse (LaTeXML Server response is invalid JSON.): J^{{-1}}={\frac {1}{\eta }}{\begin{pmatrix}\Delta y_{2}\,\Delta z_{1}\,\Delta z_{3}-\Delta y_{3}\,\Delta z_{1}\,\Delta z_{2}&-\Delta y_{1}\,\Delta z_{2}\,\Delta z_{3}+\Delta y_{3}\,\Delta z_{1}\,\Delta z_{2}&\Delta y_{1}\,\Delta z_{2}\,\Delta z_{3}-\Delta y_{2}\,\Delta z_{1}\,\Delta z_{3}\\-\Delta x_{2}\,\Delta z_{1}\,\Delta z_{3}+\Delta x_{3}\,\Delta z_{1}\,\Delta z_{2}&\Delta x_{1}\,\Delta z_{2}\,\Delta z_{3}-\Delta x_{3}\,\Delta z_{1}\,\Delta z_{2}&-\Delta x_{1}\,\Delta z_{2}\,\Delta z_{3}+\Delta x_{2}\,\Delta z_{1}\,\Delta z_{3}\\(\Delta x_{2}\,\Delta y_{3}-\Delta x_{3}\,\Delta y_{2})\Delta z_{1}&-(\Delta x_{1}\,\Delta y_{3}-\Delta x_{3}\,\Delta y_{1})\Delta z_{2}&(\Delta x_{1}\,\Delta y_{2}-\Delta x_{2}\,\Delta y_{1})\Delta z_{3}\\\end{pmatrix}} Le système est non singulier si et seulement si le déterminant ou de manière équivalente η 𝜂 est différent de zéro.

Cinématique directe

Le système d'équations de polynômes du second degré issu de la fermeture de la chaîne cinématique:

L 2 = ( x - x i ) 2 + ( y - y i ) 2 + ( z - z i ) 2 superscript 𝐿 2 superscript 𝑥 subscript 𝑥 𝑖 2 superscript 𝑦 subscript 𝑦 𝑖 2 superscript 𝑧 subscript 𝑧 𝑖 2 représente l'intersection de trois sphères de rayon L 𝐿 et de centre P i subscript 𝑃 𝑖 . L'intersection de ses sphères donne la position de la nacelle en fonction de la position des bras. La résolution de ce système d'équations est parfois appelé trilateration dans la littérature. Afin de résoudre ce système d'équations, nous allons effectuer un changement de repère qui va simplifier les calculs. La nouvelle origine va coïncide au point P 1 subscript 𝑃 1 . L'axe des X pointe vers le point P 2 subscript 𝑃 2 et le plan XY est porté par les trois points P i subscript 𝑃 𝑖 . L'axe des Y pointe du côté du point P 3 subscript 𝑃 3 . L'axe des Y est déterminé de manière à formé un trièdre direct. Dans ce nouveau repère les coordonnées des points P i subscript 𝑃 𝑖 s'écrivent: 𝒫 1 = ( 0 0 0 )   𝒫 2 = ( d 0 0 )   𝒫 3 = ( i j 0 ) formulae-sequence subscript 𝒫 1 0 0 0 formulae-sequence subscript 𝒫 2 𝑑 0 0 subscript 𝒫 3 𝑖 𝑗 0 et le système d'équations devient: L 2 = x 2 + y 2 + z 2 L 2 = ( x - d ) 2 + y 2 + z 2 L 2 = ( x - i ) 2 + ( y - j ) 2 + z 2 superscript 𝐿 2 absent superscript 𝑥 2 superscript 𝑦 2 superscript 𝑧 2 superscript 𝐿 2 absent superscript 𝑥 𝑑 2 superscript 𝑦 2 superscript 𝑧 2 superscript 𝐿 2 absent superscript 𝑥 𝑖 2 superscript 𝑦 𝑗 2 superscript 𝑧 2 Note concernant la résolution d'un système d'équations: si f ⁢ ( x , y ) = 0 𝑓 𝑥 𝑦 0 et g ⁢ ( x , y ) = 0 𝑔 𝑥 𝑦 0 alors le système f ⁢ ( x , y ) - g ⁢ ( x , y ) = 0 𝑓 𝑥 𝑦 𝑔 𝑥 𝑦 0 et f ⁢ ( x , y ) = 0 𝑓 𝑥 𝑦 0 est équivalent au premier, càd. à la seule condition que l'on conserve une des deux équations car la différence de deux nombres implique qu'ils sont égaux mais pas nulles. Pour résoudre ce nouveau système d'équations, on commence par soustraire la première et la deuxième équation et on résout pour x 𝑥 , il vient: x = d 2 𝑥 𝑑 2

On réinjecte ce résultat dans la première équation et on obtient l'équation d'un cercle correspondant à l'intersection des deux premières sphères:

z 2 + y 2 = L 2 - d 2 2 superscript 𝑧 2 superscript 𝑦 2 superscript 𝐿 2 superscript 𝑑 2 2

Notez que cette équation à une solution réelle si d ≤ 2 ⁢ L 𝑑 2 𝐿 .

À présent on substitue z 2 = L 2 - x 2 - y 2 superscript 𝑧 2 superscript 𝐿 2 superscript 𝑥 2 superscript 𝑦 2 dans l'équation de la troisième sphère et on résout pour y 𝑦 :

y = i 2 + j 2 2 ⁢ j - i j ⁢ x = i 2 + j 2 - i ⁢ d 2 ⁢ j 𝑦 absent superscript 𝑖 2 superscript 𝑗 2 2 𝑗 𝑖 𝑗 𝑥 missing-subexpression absent superscript 𝑖 2 superscript 𝑗 2 𝑖 𝑑 2 𝑗

À présent nous avons résolut les deux premières coordonnées et nous pouvons tirer la troisième à partir de l'équation du la première sphère:

z = ± L 2 - x 2 - y 2 = ± L 2 - d 2 4 - ( i 2 + j 2 - i ⁢ d 2 ⁢ j ) 2 𝑧 absent plus-or-minus superscript 𝐿 2 superscript 𝑥 2 superscript 𝑦 2 missing-subexpression absent plus-or-minus superscript 𝐿 2 superscript 𝑑 2 4 superscript superscript 𝑖 2 superscript 𝑗 2 𝑖 𝑑 2 𝑗 2

Notez que cette solution est réelle si et seulement si la troisième sphère et le cercle ont une intersection, càd. si la racine est positive ou nulle.

Afin d'exprimer les coordonnées de la solution dans le référentiel d'origine, nous allons exprimer le changement de repère:

P = P 1 + x ⁢ e ^ x + y ⁢ e ^ y + z ⁢ e ^ z 𝑃 subscript 𝑃 1 𝑥 subscript ^ 𝑒 𝑥 𝑦 subscript ^ 𝑒 𝑦 𝑧 subscript ^ 𝑒 𝑧 Le premier vecteur unitaire s'écrit: e ^ x = P 2 - P 1 ∥ P 2 - P 1 ∥ subscript ^ 𝑒 𝑥 subscript 𝑃 2 subscript 𝑃 1 norm subscript 𝑃 2 subscript 𝑃 1

et les deux premières distances:

d = ∥ P 2 - P 1 ∥ i = ( P 3 - P 1 ) ⋅ e ^ x 𝑑 absent norm subscript 𝑃 2 subscript 𝑃 1 𝑖 absent ⋅ subscript 𝑃 3 subscript 𝑃 1 subscript ^ 𝑒 𝑥

Le second vecteur unitaire s'écrit:

e ^ y = P 3 - P 1 - i ⁢ e ^ x ∥ P 3 - P 1 - i ⁢ e ^ x ∥ subscript ^ 𝑒 𝑦 subscript 𝑃 3 subscript 𝑃 1 𝑖 subscript ^ 𝑒 𝑥 norm subscript 𝑃 3 subscript 𝑃 1 𝑖 subscript ^ 𝑒 𝑥

et la troisième distance:

j = ( P 3 - P 1 ) ⋅ e ^ y 𝑗 ⋅ subscript 𝑃 3 subscript 𝑃 1 subscript ^ 𝑒 𝑦

Le troisième vecteur unitaire s'écrit e ^ z = e ^ x × e ^ y subscript ^ 𝑒 𝑧 subscript ^ 𝑒 𝑥 subscript ^ 𝑒 𝑦

Nous avons à présent résolut la cinématique directe de manière analytique, mais il n'existe pas d'expression simple de la position de la nacelle en fonction des positions des bras. C'est pourquoi nous ne chercherons pas à développer les expressions.

On définit z i ⁢ j = z i - z j subscript 𝑧 𝑖 𝑗 subscript 𝑧 𝑖 subscript 𝑧 𝑗 .

𝒫 21 = ( - 3 2 ⁢ ρ 3 2 ⁢ ρ z 21 )   𝒫 31 = ( - 3 2 ⁢ ρ - 3 2 ⁢ ρ z 31 )   𝒫 32 = ( 0 - 3 ⁢ ρ z 32 ) formulae-sequence subscript 𝒫 21 3 2 𝜌 3 2 𝜌 subscript 𝑧 21 formulae-sequence subscript 𝒫 31 3 2 𝜌 3 2 𝜌 subscript 𝑧 31 subscript 𝒫 32 0 3 𝜌 subscript 𝑧 32 ℒ 21 = 3 ⁢ ρ 2 + z 21 2   ℒ 31 = 3 ⁢ ρ 2 + z 31 2   ℒ 32 = 3 ⁢ ρ 2 + z 32 2 formulae-sequence subscript ℒ 21 3 superscript 𝜌 2 superscript subscript 𝑧 21 2 formulae-sequence subscript ℒ 31 3 superscript 𝜌 2 superscript subscript 𝑧 31 2 subscript ℒ 32 3 superscript 𝜌 2 superscript subscript 𝑧 32 2 x ⁢ e ^ x = 𝒫 21 2 = ( - 3 4 ⁢ ρ 3 4 ⁢ ρ z 21 2 ) 𝑥 subscript ^ 𝑒 𝑥 subscript 𝒫 21 2 3 4 𝜌 3 4 𝜌 subscript 𝑧 21 2 i = 𝒫 31 . 𝒫 21 d = 1 d ⁢ ( 3 2 ⁢ ρ 2 + z 21 ⁢ z 31 ) 𝑖 formulae-sequence subscript 𝒫 31 subscript 𝒫 21 𝑑 1 𝑑 3 2 superscript 𝜌 2 subscript 𝑧 21 subscript 𝑧 31 i 2 + j 2 = ℒ 31 2 = 3 ⁢ ρ 2 + z 31 2 superscript 𝑖 2 superscript 𝑗 2 superscript subscript ℒ 31 2 3 superscript 𝜌 2 superscript subscript 𝑧 31 2 y = ℒ 31 2 - 𝒫 31 ⁢ 𝒫 21 2 ⁢ 𝒫 31 . e ^ y = 3 2 ⁢ ρ 2 + z 31 2 - z 21 ⁢ z 31 2 ⁢ 𝒫 31 . e ^ y 𝑦 superscript subscript ℒ 31 2 subscript 𝒫 31 subscript 𝒫 21 formulae-sequence 2 subscript 𝒫 31 subscript ^ 𝑒 𝑦 3 2 superscript 𝜌 2 superscript subscript 𝑧 31 2 subscript 𝑧 21 subscript 𝑧 31 formulae-sequence 2 subscript 𝒫 31 subscript ^ 𝑒 𝑦 i . e ^ x = 𝒫 31 . 𝒫 21 ⁢ 𝒫 21 d formulae-sequence 𝑖 subscript ^ 𝑒 𝑥 subscript 𝒫 31 subscript 𝒫 21 subscript 𝒫 21 𝑑

Cinématique dans un plan z

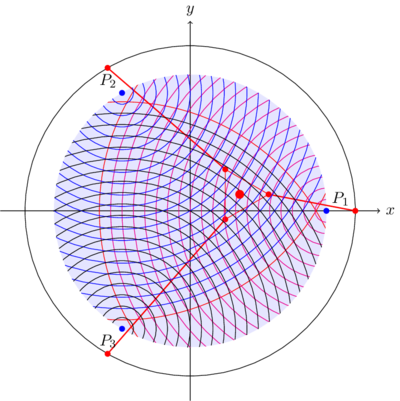
Dans le cas d'un mouvement linéaire y = α ⁢ x + β 𝑦 𝛼 𝑥 𝛽 , on obtient q i = ( x i - x ) 2 + ( y i - α ⁢ x - β ) 2 subscript 𝑞 𝑖 superscript subscript 𝑥 𝑖 𝑥 2 superscript subscript 𝑦 𝑖 𝛼 𝑥 𝛽 2 En calcul variationnel, on obtient d ⁢ q i = 2 ⁢ { ( 1 + α 2 ) ⁢ x - x i - α ⁢ y i + α ⁢ β } ⁢ d ⁢ x 𝑑 subscript 𝑞 𝑖 2 1 superscript 𝛼 2 𝑥 subscript 𝑥 𝑖 𝛼 subscript 𝑦 𝑖 𝛼 𝛽 𝑑 𝑥 via - 2 ⁢ { ( x i - x ) + α ⁢ ( y i - α ⁢ x - β ) } 2 subscript 𝑥 𝑖 𝑥 𝛼 subscript 𝑦 𝑖 𝛼 𝑥 𝛽 Dans le cas d'un mouvement circulaire ( x - x c ) 2 + ( y - y c ) 2 = C 2 superscript 𝑥 subscript 𝑥 𝑐 2 superscript 𝑦 subscript 𝑦 𝑐 2 superscript 𝐶 2 , on obtient q i = ( x i - x ) 2 + { y i - y c - C 2 - ( x - x c ) 2 } 2 subscript 𝑞 𝑖 superscript subscript 𝑥 𝑖 𝑥 2 superscript subscript 𝑦 𝑖 subscript 𝑦 𝑐 superscript 𝐶 2 superscript 𝑥 subscript 𝑥 𝑐 2 2

Conception

Châssis

  • deux plateaux en contreplaqué / Alu
  • écrous à enfoncer pour le bois
  • 6 équerres usinées en alu (axe, palier de la vis, fixation du moteur)
  • 6 paliers

Liaison glissière

La Rostock réalise la liaison glissière avec deux axes verticaux et une courroie entre les deux axes. Cette solution est assez simple, mais pas précise sans tendeur de courroie.

Solution 1 (*3):

  • un axe verticale avec coussinet
    • arbre pour guidage linéaire acier trempé et rectifié HPC p200 Za ~ 13 € en D 10 mm
    • douille à bille de précision fermée HPC p210 KBww ~ 10 €
  • une vis trapézoïdale avec un écrou en bronze
    • vis trapézoïdale acier HPC p262 ~ 10 € (fabriqué par roulage donc pas au lab)
    • écrou cylindrique bronze HPC p272 LRM ~ 13 € (usinable au lab?)
  • pièce usinée en alu
  • choisir un diamètre suffisant pour restreindre le flambage

Quel impact sur le dynamisme, puissance du moteur?

Actionneur

  • moteur pas à pas
  • accouplement:
    • HPC p38 BG ~ 20 €
    • durite de voiture

Rotule / Cardan

À priori on ne peut pas fabriquer de rotule au lab, mais des joint de cardan, oui.

Embout à rotule femelle, contact acier/bronze autolubrifiant:

  • HPC p108 CFFrh/lh ~12 € * 12 (3*2*2) => 150 € !

Autre solution d'articulation qui est usinable au lab:

  • sphère usiné au tour
  • coupelle en teflon (usiné avec une fraise sphérique)
  • porte-coupelle
  • un ressort pour maintenir l'articulation
  • mais c'est moins solide

La CNC hexapod met en œuvre des joints de cardan: avantage/inconvénient?

  • video
  • un seul bras
  • plus robuste
  • plus d'amplitude ?

Bras

Étudier une solution à base de flèche en carbone type chasse (diamètre ~ 9 mm), tige de carbone de très bonne qualité, ~ 12 € (France Archerie).

Nacelle

Pièce usinée en alu

Retrieved from "https://wiki.electrolab.fr/index.php?title=Projets:Perso:2014:Robot_Delta&oldid=12278"