Difference between revisions of "Projets:Lab:2015:Tuto VNWA:Les circuits LC"
(→Introduction à l’analyse vectorielle : Chapitre 4, Les Circuits LC) |
(→Introduction à l’analyse vectorielle : Chapitre 4, Les Circuits LC) |
||
| (One intermediate revision by one user not shown) | |||
| Line 25: | Line 25: | ||
Ohms ou « short ») et lançons un étalonnage « Open », « Load », « Short » et –pour la suite des | Ohms ou « short ») et lançons un étalonnage « Open », « Load », « Short » et –pour la suite des | ||
évènements- « Thru Cal», le tout pour une plage de mesure couvrant de 0,1 à 30 MHz | évènements- « Thru Cal», le tout pour une plage de mesure couvrant de 0,1 à 30 MHz | ||
| + | |||
Cette première étape va consister à vérifier si notre bobine se comporte effectivement comme une | Cette première étape va consister à vérifier si notre bobine se comporte effectivement comme une | ||
bobine. | bobine. | ||
| + | |||
| + | [[File:LC 1.png|900px|center|]] | ||
Nous voyons ci-dessus que notre inductance fait 2,75 μH et que son Q est de 210. Ce chiffre nous | Nous voyons ci-dessus que notre inductance fait 2,75 μH et que son Q est de 210. Ce chiffre nous | ||
| Line 50: | Line 53: | ||
- Q « chargé » ou « en charge » : si vous raccordez le circuit à quelque chose, l’énergie stockée | - Q « chargé » ou « en charge » : si vous raccordez le circuit à quelque chose, l’énergie stockée | ||
peut « s’échapper » et ainsi abaisser le niveau d’énergie contenu dans le circuit et ainsi | peut « s’échapper » et ainsi abaisser le niveau d’énergie contenu dans le circuit et ainsi | ||
| − | abaisser son Q. | + | abaisser son Q. Nous verrons plus tard, dans le chapitre consacré au « tuners et circuits |
| − | + | ||
| − | + | ||
accordés », qu’un Q fortement chargé n’est pas nécessairement une mauvaise chose. | accordés », qu’un Q fortement chargé n’est pas nécessairement une mauvaise chose. | ||
| + | |||
Q, dans les circuits résonnants, nous donne des indications sur la bande passante dudit circuit. | Q, dans les circuits résonnants, nous donne des indications sur la bande passante dudit circuit. | ||
Mais revenons un peu sur les Q chargés et hors charge : Il y a quelque chose que vous devez savoir car | Mais revenons un peu sur les Q chargés et hors charge : Il y a quelque chose que vous devez savoir car | ||
| Line 88: | Line 90: | ||
Prenons un condensateur céramique de 38 pf avec un Q de 243, et une capa variable que l’on règle à la | Prenons un condensateur céramique de 38 pf avec un Q de 243, et une capa variable que l’on règle à la | ||
même valeur | même valeur | ||
| + | |||
| + | [[File:LC 2.png|900px|center|]] | ||
| + | |||
… le condensateur variable affiche un Q de 312. Ce qui est un peu mieux. | … le condensateur variable affiche un Q de 312. Ce qui est un peu mieux. | ||
| + | |||
| + | [[File:LC 3.png|900px|center|]] | ||
Que va-t-on faire avec ces deux-là ? (la self et son condensateur associé). Relions les tout d’abord en | Que va-t-on faire avec ces deux-là ? (la self et son condensateur associé). Relions les tout d’abord en | ||
parallèle. Et comme d’habitude, en commençant avec un logiciel de simulation. (cette fois, j’ai utilisé | parallèle. Et comme d’habitude, en commençant avec un logiciel de simulation. (cette fois, j’ai utilisé | ||
RFSim) | RFSim) | ||
| + | |||
| + | [[File:LC 4.png|800px|center|]] | ||
Pas mal, n’est-ce pas ? Nous constatons une résonnance sur 15,5 MHz, ainsi qu’un truc étrange : le | Pas mal, n’est-ce pas ? Nous constatons une résonnance sur 15,5 MHz, ainsi qu’un truc étrange : le | ||
| Line 100: | Line 109: | ||
tous les deux. Si l’on se reporte aux chapitres 2 et 3, vous verrez des courbes avec de brusques | tous les deux. Si l’on se reporte aux chapitres 2 et 3, vous verrez des courbes avec de brusques | ||
montées et descentes, suivies d’une courbe montrant un changement plus progressif et plus lent. | montées et descentes, suivies d’une courbe montrant un changement plus progressif et plus lent. | ||
| + | |||
Maintenant, revenons dans le monde réel. Soudons nos deux composants entre le conducteur central et | Maintenant, revenons dans le monde réel. Soudons nos deux composants entre le conducteur central et | ||
la masse, court-circuitons le port 2 (mesure S11)… et regardons le résultat. | la masse, court-circuitons le port 2 (mesure S11)… et regardons le résultat. | ||
| + | |||
| + | [[File:LC 5.png|900px|center|]] | ||
Dans le cas présent, j’ai utilisé le condo variable. Et Paf ! ca ne ressemble en rien à notre simulation. A | Dans le cas présent, j’ai utilisé le condo variable. Et Paf ! ca ne ressemble en rien à notre simulation. A | ||
15,5 MHz, on ne voit rien. Ça doit venir du condensateur. Essayons avec l’autre | 15,5 MHz, on ne voit rien. Ça doit venir du condensateur. Essayons avec l’autre | ||
| + | |||
| + | [[File:LC 6.png|900px|center|]] | ||
| + | |||
Même résultat. Examinons pourquoi nous voyons tout ça. Un circuit résonant présente une réactance | Même résultat. Examinons pourquoi nous voyons tout ça. Un circuit résonant présente une réactance | ||
qui tend vers zéro. Donc, en montage parallèle, on peut considérer qu’à la fréquence de résonnance, le | qui tend vers zéro. Donc, en montage parallèle, on peut considérer qu’à la fréquence de résonnance, le | ||
signal est quasiment mis à la masse. A toutes les autres fréquences, il présente une impédance élevée. | signal est quasiment mis à la masse. A toutes les autres fréquences, il présente une impédance élevée. | ||
| + | |||
Mais attendez-voir… nous avons effectué une mesure S11. Donc nous voyons S11 sous l’aspect des | Mais attendez-voir… nous avons effectué une mesure S11. Donc nous voyons S11 sous l’aspect des | ||
pertes en retour. S’il y a une résonnance, la mesure de phase va nous l’indiquer. A ce point précis, les | pertes en retour. S’il y a une résonnance, la mesure de phase va nous l’indiquer. A ce point précis, les | ||
phases respectives du condensateur et de la self vont s’annuler et vont provoquer un saut de phase. | phases respectives du condensateur et de la self vont s’annuler et vont provoquer un saut de phase. | ||
| + | |||
Comme l’on pouvait s’y attendre, il survient à 15,16 MHz, presque la fréquence donnée par la | Comme l’on pouvait s’y attendre, il survient à 15,16 MHz, presque la fréquence donnée par la | ||
simulation. Donc S11 n’est pas la bonne approche. Mais pour quelle raison la simulation nous montre | simulation. Donc S11 n’est pas la bonne approche. Mais pour quelle raison la simulation nous montre | ||
| Line 120: | Line 137: | ||
Ce n’est pas un problème. Nous enlevons le bouchon qui court-circuite le support de DUT, y | Ce n’est pas un problème. Nous enlevons le bouchon qui court-circuite le support de DUT, y | ||
raccordons le port 2 et tentons une mesure S21 : | raccordons le port 2 et tentons une mesure S21 : | ||
| + | |||
| + | [[File:LC 7.png|900px|center|]] | ||
| + | |||
Bingo ! C’est ce que nous voulions voir. Nous avons notre saut de phase, nous voyons le marqueur du | Bingo ! C’est ce que nous voulions voir. Nous avons notre saut de phase, nous voyons le marqueur du | ||
| Line 131: | Line 151: | ||
Nous avons vu ce qu’était le Q. Nous n’avons pas conçu ni chargé le circuit uniquement avec une | Nous avons vu ce qu’était le Q. Nous n’avons pas conçu ni chargé le circuit uniquement avec une | ||
charge de 50 Ohms. | charge de 50 Ohms. | ||
| + | |||
| + | [[File:LC 8.png|900px|center|]] | ||
Ouvrons ici une parenthèse. Si nous construisons et assemblons le circuit correctement, nous pouvons | Ouvrons ici une parenthèse. Si nous construisons et assemblons le circuit correctement, nous pouvons | ||
| Line 137: | Line 159: | ||
bande passante est un peu plus étroite, et l’on peut constater également l’influence des fils de liaison | bande passante est un peu plus étroite, et l’on peut constater également l’influence des fils de liaison | ||
du condensateur et de la bobine. | du condensateur et de la bobine. | ||
| + | |||
| + | [[File:LC 9.png|900px|center|]] | ||
| Line 149: | Line 173: | ||
l’étalonnage sur 250 MHz que nous avons sauvegardé précédemment. Simplement pour voir ce qui se | l’étalonnage sur 250 MHz que nous avons sauvegardé précédemment. Simplement pour voir ce qui se | ||
passe. | passe. | ||
| + | |||
| + | |||
| + | [[File:LC 10.png|900px|center|]] | ||
On constate une résonance à 14,8Mhz. Ce qui nous indique que l’influence de la charge est plus | On constate une résonance à 14,8Mhz. Ce qui nous indique que l’influence de la charge est plus | ||
| Line 160: | Line 187: | ||
d’amplitude. Nous ne sommes intéressés que par les résonances de phase, lorsque ladite phase traverse | d’amplitude. Nous ne sommes intéressés que par les résonances de phase, lorsque ladite phase traverse | ||
la ligne des « Zéro degrés » à la résonance. | la ligne des « Zéro degrés » à la résonance. | ||
| + | |||
| + | [[File:LC 11.png|900px|center|]] | ||
| + | |||
Le trace ci-dessus montre un autre circuit série mais fabriqué avec un autre type de bobinage. Il | Le trace ci-dessus montre un autre circuit série mais fabriqué avec un autre type de bobinage. Il | ||
| Line 169: | Line 199: | ||
parallèle entre deux résistances de 1,5k et lancé une mesure S21. Attention, nous utilisons à nouveau | parallèle entre deux résistances de 1,5k et lancé une mesure S21. Attention, nous utilisons à nouveau | ||
une plage 5-30 MHz. | une plage 5-30 MHz. | ||
| + | |||
| + | [[File:LC 12.png|900px|center|]] | ||
Regardons tout d’abord la trace verte en Mémoire 1. Elle est atténuée par les résistances, mais montre | Regardons tout d’abord la trace verte en Mémoire 1. Elle est atténuée par les résistances, mais montre | ||
| Line 188: | Line 220: | ||
Ca y est, le mot est lâché. Les bobine fichent sacrément la frousse à la plupart des gens, et l’idée de les | Ca y est, le mot est lâché. Les bobine fichent sacrément la frousse à la plupart des gens, et l’idée de les | ||
mélanger avec d’autres composant pour faire l’objet de manipulations chamaniques en dépasse plus | mélanger avec d’autres composant pour faire l’objet de manipulations chamaniques en dépasse plus | ||
| − | d’un. Mais pas pour nous, qui sommes des VNA Supermen (ou | + | d’un. Mais pas pour nous, qui sommes devenus des VNA Supermen (ou presque) |
| − | + | ||
| − | + | [[File:LC 13.png|900px|center|]] | |
| − | |||
Prenez votre support de DUT, soudez la bobine entre les ports 1 et 2 et la capa entre le port 2 et la | Prenez votre support de DUT, soudez la bobine entre les ports 1 et 2 et la capa entre le port 2 et la | ||
| Line 217: | Line 248: | ||
== Filtre Passe-Haut == | == Filtre Passe-Haut == | ||
| + | |||
| + | [[File:LC 14.png|900px|center|]] | ||
Cette fois, le condensateur est branché entre les ports 1 et 2, et la self est reliée à la masse. Si nous | Cette fois, le condensateur est branché entre les ports 1 et 2, et la self est reliée à la masse. Si nous | ||
| Line 236: | Line 269: | ||
l’on pouvait « a contrario » voir les effets d’une désadaptation en jouant sur les termes de l’outil de | l’on pouvait « a contrario » voir les effets d’une désadaptation en jouant sur les termes de l’outil de | ||
calcul d’adaptation | calcul d’adaptation | ||
| + | |||
| + | [[File:LC 15.png|900px|center|]] | ||
Qu’est-ce qui est le plus important ? Une faible perte d’insertion bien sûr. Vous ne voulez pas voir | Qu’est-ce qui est le plus important ? Une faible perte d’insertion bien sûr. Vous ne voulez pas voir | ||
Latest revision as of 07:47, 4 April 2015
Retour à la table des matières
Introduction à l’analyse vectorielle : Chapitre 4, Les Circuits LC
Tout au long des chapitres 2 et 3, nous avons joué avec les condensateurs et les inductances. Ces deux composants peuvent servir à construire tout un tas de montages sympathiques, tels que des filtres ou des circuits oscillants. La façon de les associer et de les combiner peut varier énormément, mais la plupart du temps, on utilise des associations en mode série ou parallèle.
Nous avons vu précédemment qu’une inductance est caractérisée par une réactance qui devient de plus en plus importante au fur et à mesure qu’augmente la fréquence. Le petit copain de l’inductance, le condensateur, agit exactement de la façon contraire. Sa réactance décroit avec la fréquence. Vous imaginez ou l’on va en venir : à la recherche du point exact ou les valeurs des réactances sont égales. Car à ce point d’équilibre, il se passe des choses merveilleuses. Utilisons la notation complexe d’un tel équilibre. Par exemple 0+100 Ohms pour l’inductance et 0-100 Ohms pour le condensateur. Si l’on additionne ces deux valeurs, on obtient 0+0, ce qui signifie que la valeur de |Z| est de zéro Ohms. Si nous injectons un signal sur cette association de composant, nous nous retrouvons dans une situation qui ….
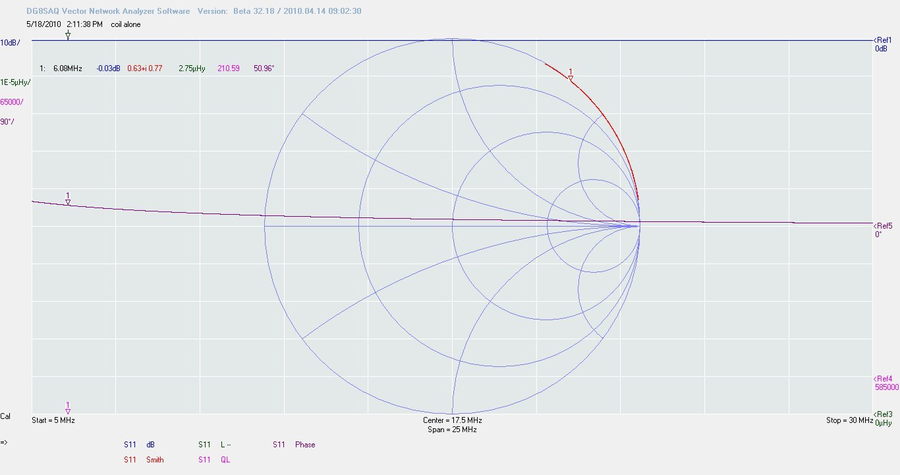
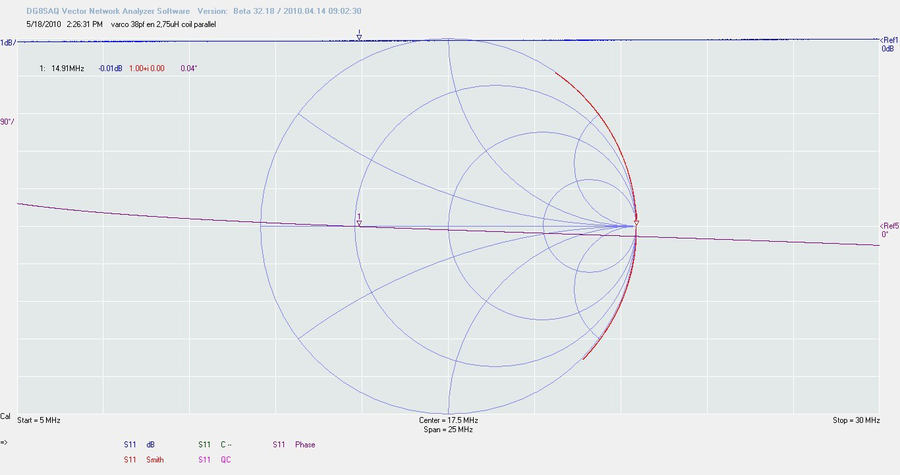
Attendez, j’ai oublié quelque chose. On a dit dès le début qu’il s’agissait d’un manuel pratique, donc passons par la pratique et prenons notre fameux support de DUT et une bobine. Soudons-la de manière à effectuer une mesure S11 (le port 2 du support de DUT « bouclé » avec le connecteur bouchon 0 Ohms ou « short ») et lançons un étalonnage « Open », « Load », « Short » et –pour la suite des évènements- « Thru Cal», le tout pour une plage de mesure couvrant de 0,1 à 30 MHz
Cette première étape va consister à vérifier si notre bobine se comporte effectivement comme une bobine.
Nous voyons ci-dessus que notre inductance fait 2,75 μH et que son Q est de 210. Ce chiffre nous donne une idée de la qualité de l’inductance. Ce chiffre nous dit que la valeur de la « part réelle » qui caractérise la bobine est faible et qu’elle ne présente que peu de perte. Si le Q avait été infiniment grand, l’énergie contenue dans son champ magnétique pourrait être maintenu pour toujours et qu’aucune puissance ne serait perdue. Mais, dans le monde réel, il y a toujours quelques résistances, quelques pertes qui font que le Q ne peut être infini. L’autre problème, c’est que le Q est utilisé pour différentes choses, dans tout un tas d’autres situations. Si vous jetez un coup d’oeil dans un bouquin ingénierie électronique, vous allez y trouver une bonne douzaine de formules pour calculer le Q. Celui des condensateurs, celui des bobines, mais également celui des cellules LC. Et ce n’est pas fini ! on fait aussi la différence entre un Q « chargé » et « non-chargé »… en fin de compte, vous ne pouvez plus vous y retrouver :-)
Pour simplifier :
- Q nous donne une idée de la capacité d’un composant à stocker de l’énergie, en d’autres termes de savoir s’il y a des pertes.
- Q « non chargé » ou « hors charge » est sa capacité à stocker de l’énergie dans une configuration isolée
- Q « chargé » ou « en charge » : si vous raccordez le circuit à quelque chose, l’énergie stockée peut « s’échapper » et ainsi abaisser le niveau d’énergie contenu dans le circuit et ainsi abaisser son Q. Nous verrons plus tard, dans le chapitre consacré au « tuners et circuits accordés », qu’un Q fortement chargé n’est pas nécessairement une mauvaise chose.
Q, dans les circuits résonnants, nous donne des indications sur la bande passante dudit circuit. Mais revenons un peu sur les Q chargés et hors charge : Il y a quelque chose que vous devez savoir car cela est d’une importance fondamentale dans le domaine de l’analyse vectorielle. Nous parlons sans cesse d’adaptation avec une charge. Alors, pour ceux qui ne sont pas ingénieurs, voici une analogie qui pourrait les aider à mieux comprendre.
Voyons les choses de la manière suivante. Une bobine est une pièce fermée, dans laquelle un paquet d’électrons excités s’agitent d’un côté et de l’autre sans trouver de chemin de sortie. Si nous ajoutons une pièce à côté de celle-ci (un condensateur), nos électrons vont courir de l’une à l’autre, mais toujours sans pouvoir s’échapper. Ajoutons que la seconde pièce est déjà aussi remplie qu’un wagon de métro à 6H du soir, et que pour qu’un électron puisse passer d’un endroit à l’autre, il faut qu’un premier électron ait déjà fait le chemin inverse et lui ait laissé sa place.
Ajoutons maintenant une troisième pièce, pratiquement vide… mais une pièce qui comporte quelques pièges mortels pour les électrons. Nous allons l’appeler la « pièce de résistance ». Nos troupeaux d’électrons vont être moins à l’étroit, et commencent à s’ébattre dans toutes les pièces à la fois. Mais ceux qui entrent dans la pièce de résistance ne reviennent jamais… et l’on doit déplorer la disparition de nos chers amis. Les électrons survivants n’apprécient pas non plus, et cette situation dégrade leur Qualité de vie.
Donc si nous chargeons la bobine ou le circuit LC avec une résistance externe, nous perdons de l’énergie, et même si le Q « hors charge » de notre circuit est très élevé, notre Q « en charge » va rapidement se dégrader. Dans un circuit LC en résonnance de caractéristiques idéales, toute l’énergie de la bobine vas dans le condensateur et vice-versa. Ce va-et-vient peut durer éternellement Mais tout ceci nous laisse entrevoir d’autres problèmes. On peut certes chercher dans certains cas à approcher d’un Q parfait pour stocker le plus d’énergie possible, mais parfois c’est l’inverse, lorsque l’on souhaite notamment que cette énergie soit transmise avec le plus d’efficacité possible. C’est notamment le cas avec les antennes. Le circuit complet doit présenter le Q le plus bas possible mais être aussi « bon » que possible. Qui a dit que la vie d’un électronicien était toujours facile ? Nous aborderons ces questions plus tard.
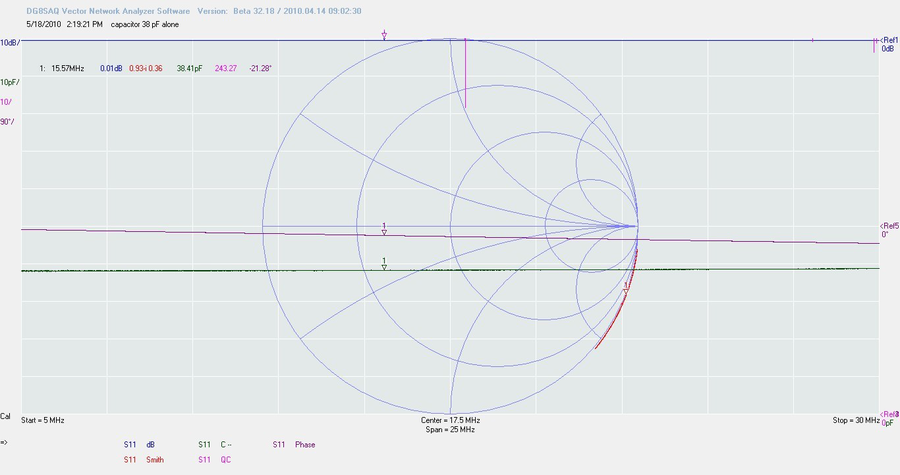
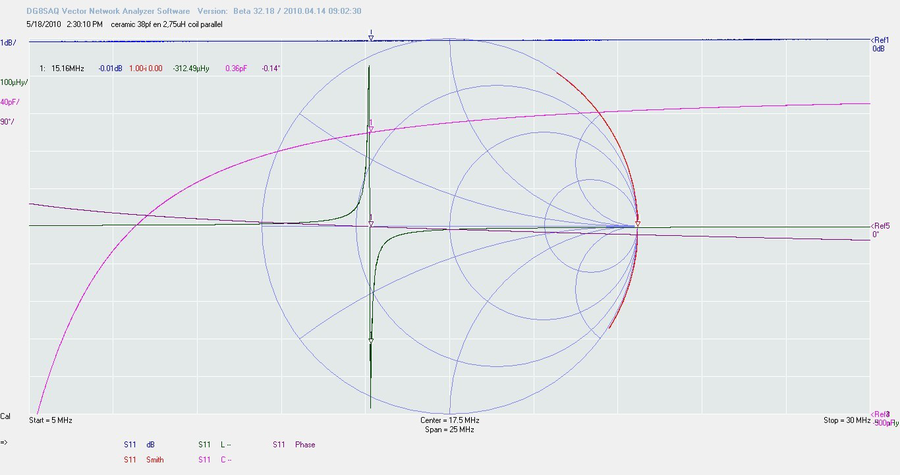
Bon, nous avons notre bobine, maintenant intéressons- nous à son copain. Prenons un condensateur céramique de 38 pf avec un Q de 243, et une capa variable que l’on règle à la même valeur
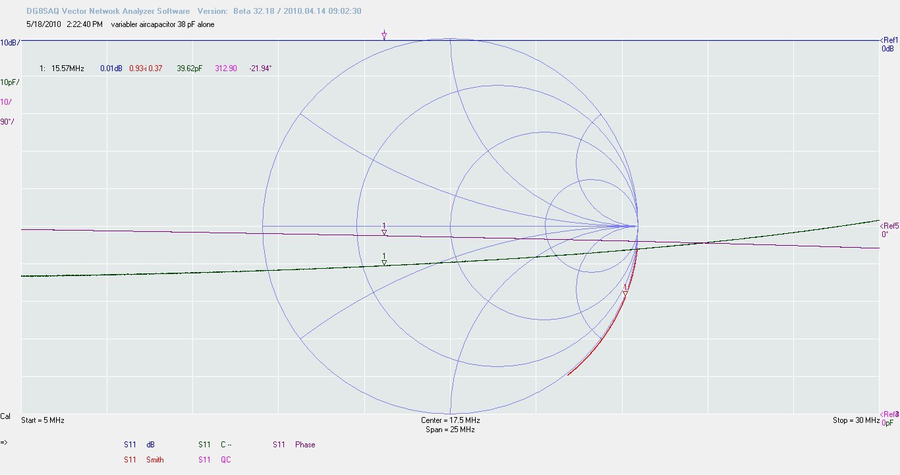
… le condensateur variable affiche un Q de 312. Ce qui est un peu mieux.
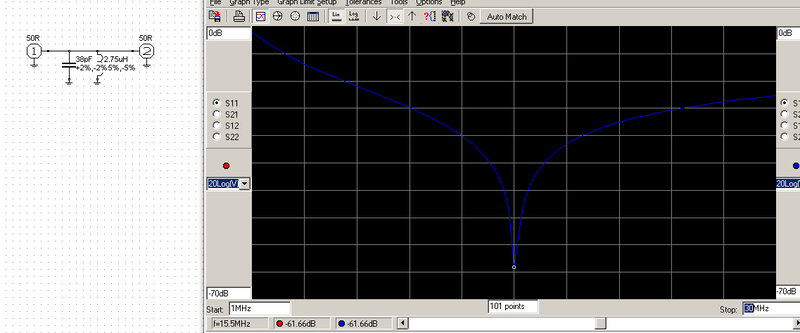
Que va-t-on faire avec ces deux-là ? (la self et son condensateur associé). Relions les tout d’abord en parallèle. Et comme d’habitude, en commençant avec un logiciel de simulation. (cette fois, j’ai utilisé RFSim)
Pas mal, n’est-ce pas ? Nous constatons une résonnance sur 15,5 MHz, ainsi qu’un truc étrange : le signal ne se comporte pas de manière symétrique La première partie est réalisée par l’inductance, la seconde principalement par le condensateur, et l’on peut constater qu’ils n’offrent pas la même pente tous les deux. Si l’on se reporte aux chapitres 2 et 3, vous verrez des courbes avec de brusques montées et descentes, suivies d’une courbe montrant un changement plus progressif et plus lent.
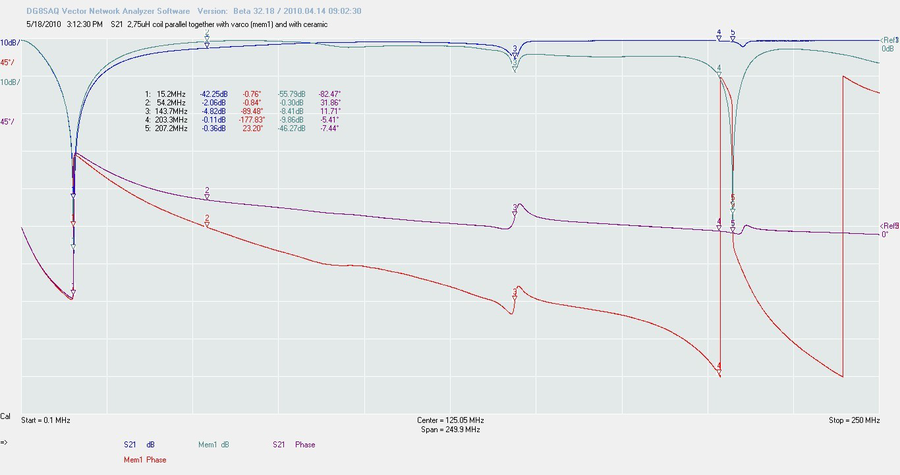
Maintenant, revenons dans le monde réel. Soudons nos deux composants entre le conducteur central et la masse, court-circuitons le port 2 (mesure S11)… et regardons le résultat.
Dans le cas présent, j’ai utilisé le condo variable. Et Paf ! ca ne ressemble en rien à notre simulation. A 15,5 MHz, on ne voit rien. Ça doit venir du condensateur. Essayons avec l’autre
Même résultat. Examinons pourquoi nous voyons tout ça. Un circuit résonant présente une réactance qui tend vers zéro. Donc, en montage parallèle, on peut considérer qu’à la fréquence de résonnance, le signal est quasiment mis à la masse. A toutes les autres fréquences, il présente une impédance élevée.
Mais attendez-voir… nous avons effectué une mesure S11. Donc nous voyons S11 sous l’aspect des pertes en retour. S’il y a une résonnance, la mesure de phase va nous l’indiquer. A ce point précis, les phases respectives du condensateur et de la self vont s’annuler et vont provoquer un saut de phase.
Comme l’on pouvait s’y attendre, il survient à 15,16 MHz, presque la fréquence donnée par la simulation. Donc S11 n’est pas la bonne approche. Mais pour quelle raison la simulation nous montre ce que nous voulons voir ?
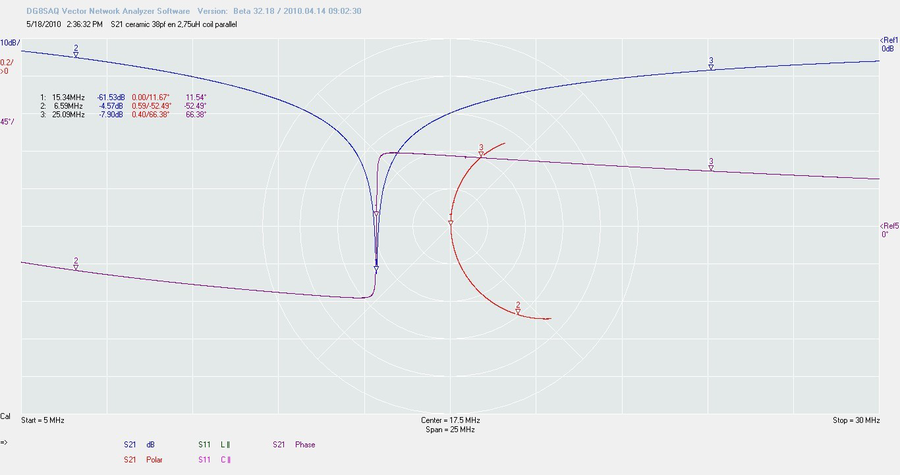
C’est simple. Dans notre cas, le circuit est « captif » entre les deux ports qui présentent une résistance de 50 Ohms en parallèle. Donc nous mesurons les pertes en retour via une résistance influencée par le montage parallèle, et qui elle-même « charge » le circuit. Nous ainsi un diviseur de tension. Ce n’est pas un problème. Nous enlevons le bouchon qui court-circuite le support de DUT, y raccordons le port 2 et tentons une mesure S21 :
Bingo ! C’est ce que nous voulions voir. Nous avons notre saut de phase, nous voyons le marqueur du
point de basculement au centre de l’abaque polaire et qui prouve qu’il est purement ohmique à la
fréquence de résonance très exactement sur 15,34 MHz… tiens-tiens… c’était pas 15,16 MHz tout à
l’heure ? Voilà qui nous montre l’influence de la charge d’un circuit sur sa fréquence de résonance. Si
vous voulez utiliser ce montage en guise de filtre, vous devez faire attention au point à 3 dB. Et l’on
rencontre à nouveau un problème. Les deux points à 3 dB sont situés en dehors de l’affichage. Ce qui
veut dire que la bande passante est supérieure aux 25 MHz affichés par la fenêtre de mesure du VNA.
25 MHz, c’est pratiquement toute la bande HF. Mais tout n’est pas si catastrophique que ça en a l’air.
Nous avons vu ce qu’était le Q. Nous n’avons pas conçu ni chargé le circuit uniquement avec une
charge de 50 Ohms.
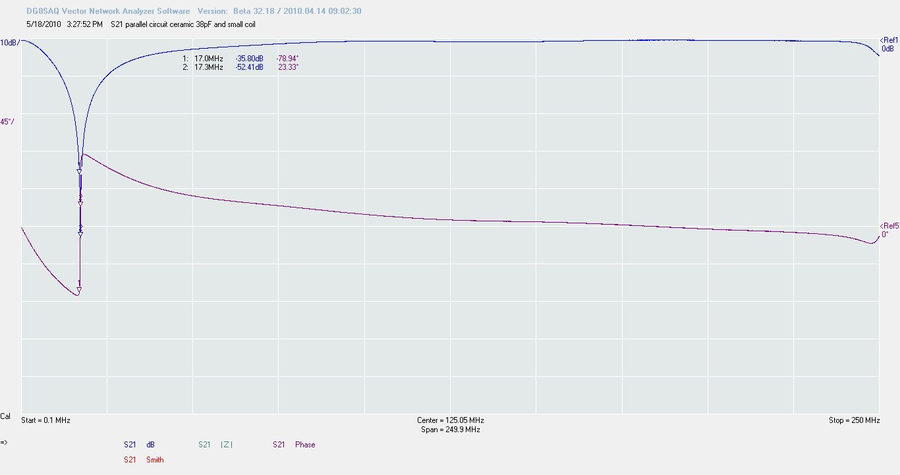
Ouvrons ici une parenthèse. Si nous construisons et assemblons le circuit correctement, nous pouvons obtenir la trace ci-dessus. Il couvre une plage de 250 MHz et ne montre aucune autre résonance comme c’est le cas dans la mesure ci-dessous. Nous voyons l’effet du Q du condensateur variable. La bande passante est un peu plus étroite, et l’on peut constater également l’influence des fils de liaison du condensateur et de la bobine.
Circuits série :
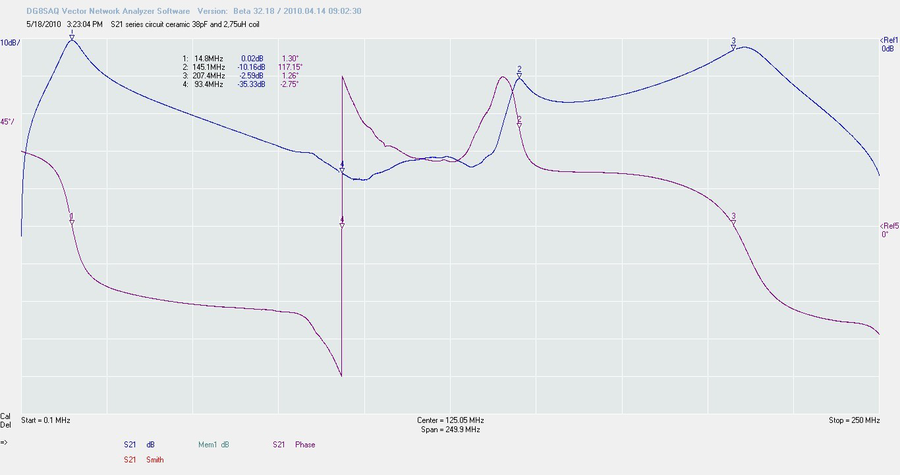
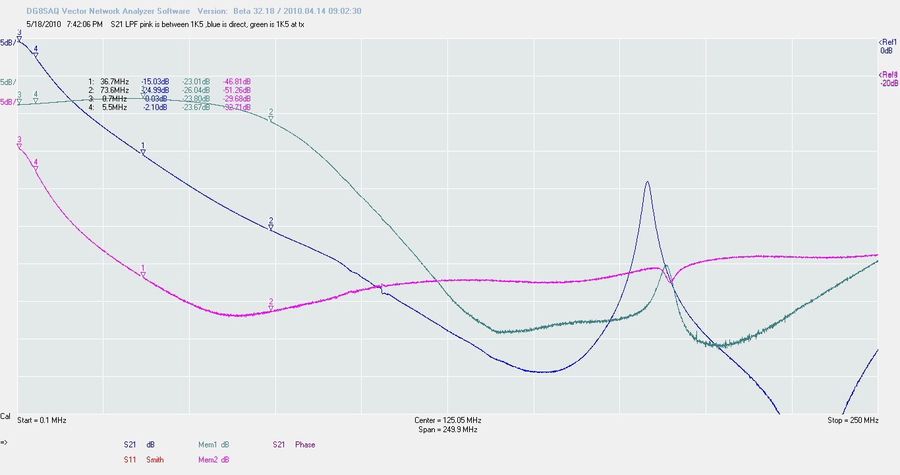
Il existe un autre type de montage L-C : l’assemblage série. Dans ce cas, l’impédance du circuit à la fréquence de résonance est également très basse et laisse passer le signal. Seulement cette vois, le circuit n’est pas relié à la masse. Les autres fréquences sont seulement atténuées par la réactance et non pas éliminées par envoie direct à la masse. Ce n’est donc pas un montage aussi efficace que le montage parallèle, mais parfois l’on a besoin d’une bande passante large. Cette fois, j’ai utilisé l’étalonnage sur 250 MHz que nous avons sauvegardé précédemment. Simplement pour voir ce qui se passe.
On constate une résonance à 14,8Mhz. Ce qui nous indique que l’influence de la charge est plus importante. Nous voyons d’autres résonances à 93 MHz. Une résonance parallèle alors que nous utilisons un montage série : on doit donc en conclure qu’il s’agit là de la conséquence d’éléments parasites. Voilà qui pourrait s’avérer relativement dangereux si cet assemblage était utiliser dans un ampli VHF, car il aurait tendance à osciller à 93 MHz.
On retrouve également un résonnance série sur 145 et 207 MHz. La dernière est une véritable résonance. Regardez la phase qui le prouve. Celle sur 145 MHz est ce que l’on appelle une résonance d’amplitude. Nous ne sommes intéressés que par les résonances de phase, lorsque ladite phase traverse la ligne des « Zéro degrés » à la résonance.
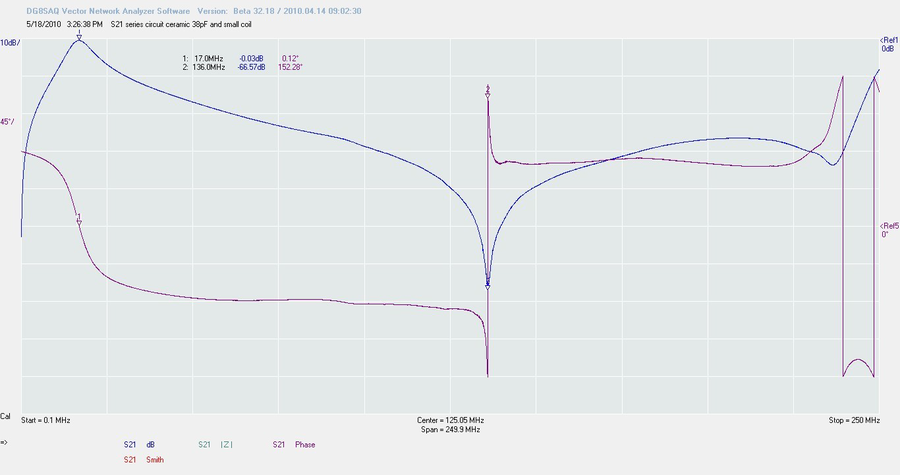
Le trace ci-dessus montre un autre circuit série mais fabriqué avec un autre type de bobinage. Il
montre une résonance parallèle très importante. Ce n’est donc pas un circuit bien monté. Qu’ai-je fait
pour obtenir cela ? J’ai pratiquement posé la self sur le plan de masse, créant ainsi un effet capacitif en
parallèle avec la bobine.
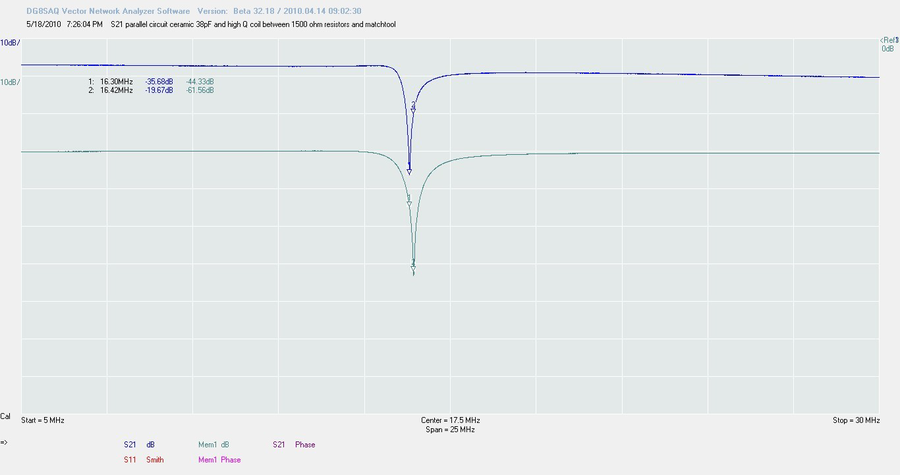
Maintenant, tentons d’améliorer les choses. Nous devons décharger le circuit. J’ai inséré un montage parallèle entre deux résistances de 1,5k et lancé une mesure S21. Attention, nous utilisons à nouveau une plage 5-30 MHz.
Regardons tout d’abord la trace verte en Mémoire 1. Elle est atténuée par les résistances, mais montre un creux plus prononcé que lors de la mesure précédente. Mais nous souhaitons corriger la désadaptation. Donc, après avoir enregistré une mesure port 2 dans le buffer S2P, nous lançons l’outil de calcul d’adaptation d’impédance (menu Tools/Matching Tool). Entrons 1500 Ohms dans les deux fenêtres « port 1 » et « port 2 », et regardons le résultat sur la trace 2. La bande passante est bien meilleure.
Voilà donc une chose avec laquelle il faut tenir compte. Si nous utilisons un tel circuit en entrée d’un récepteur, il verra 50 Ohms en entrée et en sortie. Son efficacité sera quasiment nule. Si nous l’intégrons en revanche entre deux amplis buffer à haute impédance, le circuit ne sera pratiquement pas chargé, et nous aurons un filtre qui sera capable de remplir sa fonction avec rien de plus qu’un circuit en montage parallèle. Une autre solution consisterait à dessiner un filtre utilisant une combinaison de montages L et C capables à la fois de jouer le rôle de filtre et d’adaptateur d’impédance tout à la fois.
Les filtres, ou comment employer un montage LC avec astuce Ca y est, le mot est lâché. Les bobine fichent sacrément la frousse à la plupart des gens, et l’idée de les mélanger avec d’autres composant pour faire l’objet de manipulations chamaniques en dépasse plus d’un. Mais pas pour nous, qui sommes devenus des VNA Supermen (ou presque)
Prenez votre support de DUT, soudez la bobine entre les ports 1 et 2 et la capa entre le port 2 et la
masse. Ouvrez le fichier d’étalonnage 250 MHz et lancez une mesure S21. Cela doit donner quelque
chose comme le tracé ci-dessus Qu’est-ce qui se passe ? La bobine atténue les fréquences au fur et à
mesure que celles-ci augmentent. Mais sous la bobine s’est créée une capa parasite en entre la self et la
masse. Elle forme une réactance qui diminue au fur et à mesure que croît la fréquence. Les fréquences
basses ne sont pas affectées, mais les hautes commencent à cafouiller. L’on vient de fabriquer un filtre
passe-bas. Regardons les tracés :
La ligne bleue qui décline montre l’efficacité du filtre passe-bas. On ne peut pas dire que le filtre soit
franchement abrupt, et la plage qui présente le moins de pertes est assez étroite. Mais le filtre fait sont
travail.
La ligne verte montre ce même filtre avec une 1,5 k en série du coté du port RX (sortie). La courbe du filtre en est toute changée
La ligne rose montre encore ce même filtre mais avec deux résistances de charge de 1k5, l’une en entrée, l’autre en sortie. Voilà qui nous montre clairement les effets d’une désadaptation et d’une charge, et nous apprend qu’il ne faut jamais brancher un vna directement à un filtre. L’on doit avant tout connaitre les impédances d’entrée et de sortie. L’outil de calcul d’adaptation intégré dans le logiciel de DG8SAQ est d’une grande aide dans de telles conditions. Je le montrerais au cours d’une prochaine expérience.
Filtre Passe-Haut
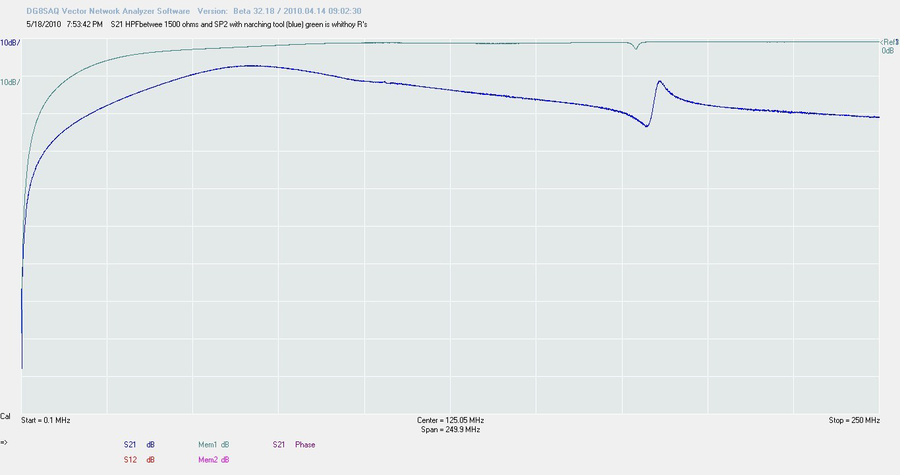
Cette fois, le condensateur est branché entre les ports 1 et 2, et la self est reliée à la masse. Si nous branchons notre instrument sans avoir la moindre idée de l’impédance du circuit (les deux résistances du chapitre précédent), la courbe du filtre est celle donnée par le tracé bleu. Pas de quoi sauter au plafond : le montage atténue le signal sur toute la plage de mesure.
Mais après une mesure « deux ports », exécutons l’outil de calcul d’adaptation. Il suffit de cliquer sur l’un des champs, puis de faire tourner le bouton du milieu de la souris pour voir la courbe se déformer. L’on peut ainsi rechercher la forme la plus optimale du filtre, à savoir celle qui présente l’atténuation la plus faible aux fréquences hautes et la plus forte aux fréquences basses. En plaçant le filtre entre deux résistances de 1k5, on obtient la courbe verte. Ce filtre est affecté par des capacités et inductances parasites, qui à leur tour peuvent être compensées à l’aide de ce même outil d’adaptation, mais nous ne nous lanceront pas dans une telle opération aujourd’hui.
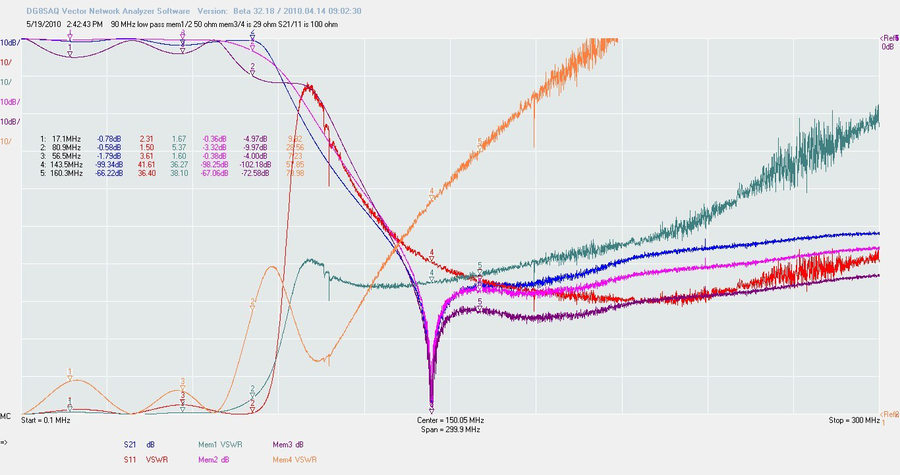
Voici ci-après un autre montage de test. Il s’agit d’un filtre 90 MHz comptant 5 cellules de filtrage LC/ Le circuit a été conçu pour présenter une impédance d’environ 50 Ohms. Mais ce serait bien si l’on pouvait « a contrario » voir les effets d’une désadaptation en jouant sur les termes de l’outil de calcul d’adaptation
Qu’est-ce qui est le plus important ? Une faible perte d’insertion bien sûr. Vous ne voulez pas voir atténué le signal situé dans la bande passante du filtre. Vous voulez également une atténuation franche et la plus raide possible. Et pour couronner le tout, un taux de pertes en retour (vswr) le plus faible possible dans la plage « passante » du filtre. Chaque section de filtre que vous ajouterez (créant ainsi un filtre avec un ordre plus élevé) améliorera le coude d’atténuation et la pente de « coupure » du filtre (exprimée en dB/octave).
La trace bleue est celle du filtre « tel quel ». La perte d’insertion, causée par l’ondulation de plateau du filtre, et un peu élevée dans le cas présent. J’ai découvert après coup que l’un de mes câbles utilisé durant la mesure n’était pas parfait et provoquait quelques pertes et retours. Normalement, cette atténuation est inférieure à 0,1 dB. Le coude et la pente du filtre sont francs, et l’atténuation hors bande est située entre -50 et -100 dB
Maintenant, passons à la trace mauve, Mem3 (et 4 pour les pertes en retour). J’ai indiqué au VNA que le filtre présentait une impédance de 20 Ohms. Si nous utilisons ce filtre à 20 Ohms, nous constatons une ondulation très prononcée et pratiquement 5 dB de pertes d’insertion, ce qui est énorme. Le bon côté des choses, c’est que l’atténuation hors bande est nettement améliorée, mais les pertes en retour (vswr) et les pertes d’insertion sont telles que le filtre est inutilisable. Il nous montre simplement l’importance que prend une bonne adaptation d’impédance. J’insiste sur le fait que rien n’a été changé dans le circuit du filtre lui-même.
La trace rose, Mem2 et Mem1, a une bonne tête, trop bonne d’ailleurs, ce qui est le signe que quelque chose ne vas pas. C’est la raison pour laquelle je n’ai pas poursuivi la mesure après réparation. Ce tracé nous apprend qu’il ne faut jamais faire confiance en son équipement ; testez-le toujours avant chaque séries de mesures. J’ai effectué une mesure « Through » avec chaque câble, et le coax du port RX a montré des pertes indésirables provoquées par un connecteur mal serti (par moi). Donc jamais d’exception : commencez chaque session de mesure avec une mesure SOLT. Les trois premières mesures (short, open et load) doivent inscrire un point fixe à la bonne place sur l’abaque de Smith. Le Through calle la courbe d’une perte d’insertion nulle. Si tout est OK, vous êtes paré pour entamer les réjouissances… et attaquer le chapitre 5. Ou l’on reparlera d’histoires de Q.
A suivre…
Fred PA4TIM
L’original de ce texte est disponible à l’adresse
http://www.pa4tim.nl/wp-content/uploads/2010/11/VNA_hfst4_resonant_cuitcuits.pdf
L’intégralité du didacticiel est accessible à l’adresse
Le contenu de ce texte ne peut être modifié sans l’autorisation de son auteur. Traduction f6itu sous Creative Commons