Projets:Lab:2015:Tuto VNWA:Les Selfs
Retour à la table des matières
Introduction à l’analyse vectorielle : Chapitre 2, Les Inductances
Les inductances sont des composants que l’on utilise souvent en radio. Nous les mesurons avec un RLC-mètre… puis nous nous dépêchons de monter un circuit avec elles dans le seul but de savoir si leur résonance est éloignée ou non de la valeur calculée. Les raisons de cet écart quasi certain sont nombreuses. Certaines sont en rapport direct avec ce que nous avons vu au cours du premier chapitre, mais il en existe d’autres qui sont directement liées au caractère fondamentalement vicieux des caractéristiques propres aux inductances.
La première chose qui cloche, c’est qu’une inductance n’a pas de valeur fixe. Celle-ci dépend de la phase du signal, et par conséquent de la fréquence de ce même signal. Les scientifiques se sont mis d’accord sur le fait que l’on devait mesurer une inductance entre +45 et +60 degrés. Ceci en raison du comportement du rapport entre courant et tension. Le courant commence à s’écouler, et ensuite seulement la tension augmente. Ce retard est de 90 degrés, et il s’agit là d’une moyenne approximative. Entre 45 et 60 degrés, le coefficient de self-induction varie relativement peu, donc l’angle considéré n’a pas trop d’importance.
Nos chers RLC mètres effectuent des mesures sur une ou deux fréquences. Cette mesure est généralement correcte, car la phase ne change que très lentement à ces fréquences basses. Mais la bobine possède des caractéristiques qui la font se comporter tout autrement sur d’autres fréquences. Et c’est précisément ce que nous allons voir expérimentalement. Partons à la découverte de l’inductance
Configuration du VNA
Nous allons reprendre notre support de DUT et fabriquer 4 bobines différentes. L’une sera un bobinage en l’air, théoriquement parfait. La première photo nous la montre, nous l’appellerons « Bobine A ». La « Bobine B » sera faite sur un tore en matériau 4C6, et la troisième, « Bobine C » utilisera un tore T32-2. La dernière, « Bobine D », est une self récupérée sur un vieux BCL. Pour suivre cet exercice, ne vous préoccupez pas du matériau servant de support. Construisez-les avec ce que vous avez sous la main, en tentant de trouver quelque chose d’approchant ce qui vous permettra de « traduire » aisément les résultats et les interprétations. Le résultat n’en sera même que plus pédagogique si vos selfs sont différentes des miennes.
Tout d’abord, voyons ce qu’est capable de faire une inductance.
Une inductance idéale présente une réactance pure, autrement dit une résistance au courant alternatif. La notation complexe de son impédance R+xj devrait être de 0+100j. Soit 100 Ohms de réactance. Il ne devrait pas y avoir de résistance pure (la partie R) et, au fur et à mesure que la fréquence s’élèvera, il en sera de même pour la réactance. Donc on peut s’attendre à une atténuation qui va augmenter avec la fréquence. La trace S21 va chuter de manière linéaire. Voyons si c’est réellement le cas.
Utilisons en premier lieu la bobine D. Nous réglons notre support de DUT pour une mesure S21 (voir première photo, self montée entre les prises TX et RX du support de DUT). On effectue tout d’abord un vrai étalonnage de notre support de DUT comme indiqué au cours du premier chapitre, avec un morceau de fil pour faire le « thru » et le « short ». Sauvons ce point d’étalonnage avec un nom particulier (exemple SupportDUT_S21_250 MHz)… nous allons être amenés à l’utiliser très souvent.
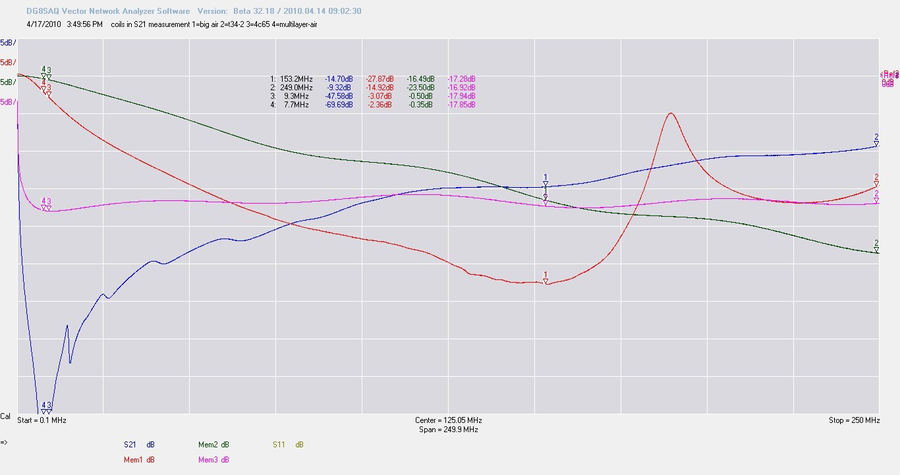
Coté VNA, on sélectionne S21 en dB et on lance un balayage couvrant 0,1 à 250 MHz. On jette un oeil
sur la courbe… ça fait peur, pas vrai ? Appelons la bobine D FrankenSelf. Sa trace –bleue à l’écranplonge
d’un coup puis remonte progressivement alors que nous nous attendions précisément à ce
qu’elle diminue avec l’augmentation de fréquence. Probablement un effet du côté obscur de la Force.
Mais avant de la combattre, testons nos autres bobinages.
Vous pouvez constater que la bobine la plus « idéale » est la bobine B. Par la suite, nous verrons qu’elle n’est pourtant pas la meilleure.
Tout ça veut dire qu’il y a quelques caractéristiques qui entrent en jeu et qui ne sont pas facilement discernables Les deux bobines sur tores se ressemblent même, mais montrent des comportements différents.
La bobine A –Mem1, trace rouge- se comporte normalement jusqu’à 153 MHz. A partir de là, la trace se met à monter. C’est la même réaction que l’on a constaté sur la bobine D, trace S21 bleue, à la seule différence près que cette dernière plonge pour atteindre son minimum à 7,7 MHz, puis se met à remonter à partir de cette limite. La bobine C, Mem3, en rose, plonge également à 9,3 MHz mais ne remonte pas franchement. Bizarre. 4 bobines, 4 réactions différentes. Pour découvrir pourquoi, nous devons explorer les caractéristiques cachées. Et pour le faire, nous allons nous lancer dans une seconde expérimentation. Bienvenu dans le monde des comportements parasites.
Mesure S11
La première étape consiste à étalonner notre support de DUT (voir le chapitre 1). Pour ce faire, nous déconnectons le connecteur situé du côté du « port RX », y plaçons un bouchon (prise « short »), et lançons successivement un étalonnage « Open » (le support est « ouvert » puisqu’aucun composant n’y est soudé), puis un étalonnage « Short » (en soudant une queue de composant reliant les deux segments de piste centrale) et enfin un étalonnage « Load » en remplaçant le strap utilisé pour le calibre « short » par une paire de résistances de 100 Ohms en parallèle –ou par une résistance de 50 Ohms si vous en possédez une-. Sauvegardez les données de l’étalonnage en lui donnant un nom facile à retenir (exemple SupportDUT_S11_250 MHz), il sera fréquemment utilisé au fil des prochains chapitres.
L’on aurait pu utiliser une autre technique, plus simple encore, qui consiste à souder le tore directement sur une prise BNC (voir photo ci-dessus). Cette méthode n’est mentionnée que pour mémoire, et nécessite pas mal de précautions, notamment celle consistant à ne pas effectuer de mesure au-dessus d’une surface métallique.
interpréter étant relativement élevé, je vais reprendre les mesures bobine par bobine et vous guider
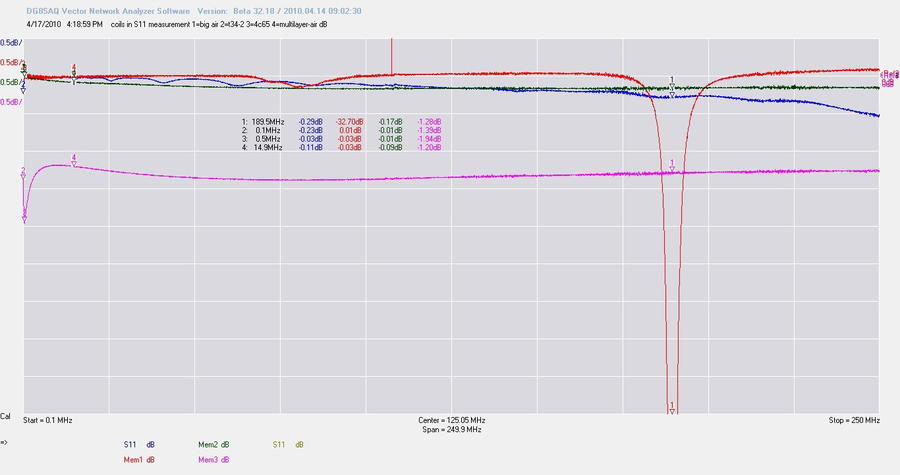
dans ce labyrinthe fait de détails cachés(cliquez sur la photo pour agrandirCe tracé des pertes par réflexion nous fournit cependant quelques indices. La trace rouge nous montre un creux très net. Les pertes par réflexion ont un rapport avec l’impédance. Une perte par réflexion d’environ 30 dB correspond à une impédance d’à peu près 50 Ohms. Une perte par réflexion nulle indique une impédance soit très haute soit très faible. Une réactance pure (une impédance sans la moindre résistance) nous donnera 0 dB. Revenons à notre trace rouge, avec son plongeon à 50 Ohms. Ce creux est marqué à la même fréquence que le « dos d’âne » que nous avions constaté en mesure S21. Il s’agit en fait du même effet mais avec une autre représentation : l’impédance chute au lieu de croître et indique qu’il y a là une probable résonance à la fréquence donnée. Mais attention, tous les accidents sur une telle courbe ne sont pas nécessairement des résonances. Ils peuvent être provoqués par une mesure fausse ou un mauvais étalonnage. Ajoutons que si la courbe ne suit pas un tracé à 0 dB, c’est qu’il y a perte.
Mais alors, mieux comprendre ce phénomène ? le VNA possède un nombre important d’options destinées à améliorer l’examen de ces inductances. S’il y a une réelle résonance, l’on doit aussi observer un changement de phase et, sur l’abaque de Smith, le tracé doit quitter le secteur « inductif » (souvenez-vous, la partie « haute », comme H, Henry) de l’abaque et pénétrer dans la zone capacitive. La résonance se situe au point exact ou la courbe passe d’un secteur à l’autre, là où les composantes inductives et capacitives sont aussi importantes l’une que l’autre et arrivent à s’équilibrer. Ce qui reste n’est qu’une valeur purement résistive (l’on peut également effectuer une mesure S21 pour le voir) Ci-dessus, la référence zéro degrés est située sur la ligne de repère en milieu d’écran. On peut voir deux sauts de phase nets et d’autres changements moins évidents.
La ligne bleue, sur 7,8 MHz, et la rouge, à 188 MHz sont faciles à repérer. La ligne rose franchit également la ligne des « zéro degré » mais ce n’est pas ce que l’on peut appeler un « saut ». Généralement, lorsque l’on veut obtenir une résonance dans un circuit, on fabrique un réseau avec une inductance et un condensateur. Ces tracés laissent entendre qu’il y aurait un condensateur « caché » dans ces bobinages. Mais je n’ai rien caché du tout. Il était là sous nos yeux depuis le début. La bobine oppose une réactance au signal. Cette « résistance » augmente avec la fréquence. Mais les spires des bobines sont proches l’une de l’autre. Un signal injecté dans la self provoque une élévation de tension aux bornes du bobinage. Donc, il se crée un champ électrique entre les enroulements. Deux portions de fil situées en regard l’une de l’autre et parcourues par ce champ peuvent être considérées comme les deux électrodes d’un condensateur et forment effectivement un effet capacitif. Or un condensateur présente une plus faible résistance aux signaux alternatifs au fur et à mesure que la fréquence augmente. Il arrive donc un point à partir duquel la capacité parasite entre spires constitue pour le signal un passage plus « facile » pour aller d’une extrémité à l’autre de la self. Le point ou la résistance aux signaux alternatifs présenté par l’inductance elle-même d’une part, et les capacités parasites d’autre part est strictement égale est le point de résonance.
Maintenant, regardons les selfs les unes après les autres :
Bobine A:
La bobine A est une self à air à spires non jointives. Ses enroulements sont espacés d’une distance d’environ un diamètre de fil. Que pouvons-nous dire à l’examen de la capture ? Nous voyons 5 traces. S11 en dB (bleue) sert de référence. La phase (rouge) est indiquée en degrés, L// est l’inductance parallèle (vert sombre) exprimée en μH, le Q, ou facteur de qualité de la bobine(en mauve) et l’abaque de Smith en vert olive. Gardons à l’esprit qu’il s’agit d’une mesure de réflexion (S11). C’est pourquoi la phase –trace rouge- va se comporter différemment qu’en mesure S21. Cette courbe est très pratique pour situer l’endroit où nous allons mesurer l’inductance. La mesure doit s’effectuer entre 45 et 60 degrés. Ici, nous allons prendre 52 degrés (marqueur 1, gauche de l’écran). L’inductance est de 1,77 μH. En mesurant cette même inductance avec mon LRCmètre, j’ai effectivement obtenu un résultat identique : 1,77μH à 100 kHz. Mais le graphique nous montre d’autres choses, car S11 traverse la ligne médiane du « zéro degrés » en deux endroits. Aux environs de 86 et de 160 MHz. Le premier point n’est pas très important. Il est accompagné par un léger « creux » de la trace S11. Rien de très significatif, mais regardons à la fois le tracé de l’abaque de Smith ainsi que celui de l’inductance (courbe verte). La valeur de la self grimpe comme une fusée, et un instant après, le tracé de la Smith s’enfonce dans la zone capacitive. Mais si l’on continue à augmenter la fréquence, le tracé de la Smith remonte en direction du secteur inductif. La trace s’infléchit vers son centre de rotation, et pénètre dans la zone inductive en franchissant la ligne médiane très exactement sur le point des 50 Ohms, comme le laissait prévoir le tracé S2. Ce qui signifie qu’outre la capacité, l’on est face également à une composante résistive, ou perte. C’est là la résistance du cuivre et des « effets de peau ». Car les ondes préfèrent se propager sur la surface externe d’un conducteur. D’autres facteurs de perte entrent en jeu, notamment ceux apportés par l’isolant recouvrant le fil de la bobine. Si vous utilisez ce bobinage audessus de 86 MHz, il faut vous attendre ce qu’il vous fasse perdre de la puissance. En temps normal, un inducteur pur ne doit pas dissiper la moindre puissance. Ceci dit, si vous vous contentez d’utiliser cette self uniquement en HF, elle fera du très bon travail, et offrira un Q élevé. Sur ces fréquences, les pertes seront faibles, et « Bobine A » pourra être qualifiée de self presque parfaite, avec un Q de 160 à 9 MHz. Son tracé en terme d’inductance semble relativement plat sur toute la bande HF, mais l’échelle est trompeuse, avec 10μH par graduation. A 30 MHz, cette bobine présente une inductance de 4 μH. Ce qui la rend inutilisable dans un filtre ou un circuit accordé travaillant sur cette fréquence. La trace « Q » a été renvoyée en-deçà de l’affichage, car elle devient totalement folle passé la limite des 80 MHz, et aurait rendu impossible la lecture des autres mesures. Mais la valeur de Q peut être lue parmi les données des marqueurs (valeur inscrite en mauve). Cela est-il suffisant et significatif ? Oui, car cette mesure ne vous indique pas seulement la valeur de l’inductance à une fréquence précise, mais vous apprend si le composant réagit encore comme une bobine, ainsi que son facteur de qualité. De cette façon, vous savez estimer les pertes éventuelles et avoir une idée de sa bande passante.
Bobine B:
Cette inductance est faite de 12 tours sur un tore T34-2 en poudre de fer (du moins je pense). C’est le petit frère du fameux T200-2 que certains apprécient pour fabriquer des choke ou des baluns. Des utilisations qui demandent un coefficient de self-inductance assez fort.
Lors de la mesure S21, la bobine B avait montré de bonnes caractéristiques. Nous ne voyons aucune résonance jusqu’à 250 MHz… elles surviennent juste au-dessus de cette limite. La valeur de l’inductance est relativement petite, à 580 nH… et difficile d’aller plus loin, il n’y a plus assez de place pour y caser plus de fil sans favoriser la capacitance du composant.
Si vous regardez la courbe de Smith avec attention, vous remarquerez que la trace a tendance à pénétrer du côté « intérieur » du cercle extérieur. Souvenez-vous du chapitre 1 : cela signifie que nous avons là une composante résistive. On peut également constater cet effet en examinant le Q (facteur de qualité) de la bobine, qui est de 112 à 9 MHz. La bobine A affichait 160 à cette même fréquence, et avec bien plus de spires encore. Du coup, j’ai ajouté un tracé C// pour indiquer la capacitance. En dessous de 50 MHz, cette capacitance affiche une valeur négative importante, ce qui est une bonne chose. Mais sur des fréquences plus hautes, elle diminue fortement pour n’être plus qu’à quelque pF de la limite inductive-capacitive. La marge de stabilité devient étroite. Si l’on installe cette bobine audessus d’un plan de masse, son état d’inductance presque parfaite va rapidement se dégrader. Mais ce genre de bobine est fait pour fonctionner sur des fréquences basses, et notre composant peut faire une jolie petite self dans un filtre passe-bande par exemple
Bobine C:
C’est le petit frère d’un tore 4C65. Son coefficient de self-induction est élevé, à 156 μH à 100 kHz, malgré ses 9 spires seulement. Les pertes sont aussi élevées que l’est l’induction, ce que l’on peut également constater sur la trace S11 en dB ainsi que sur l’abaque de Smith. L’une des conséquences est un Q assez mauvais, qui ne dépasse pas 5. Dans certaines applications, tout çà n’est pas très bon, mais ce tore est parfait pour faire une choke large bande de réjection en mode commun. Elle vous offre une self-induction élevée sur toute la largeur de la bande HF. La trace L// (ainsi que le point de franchissement « zéro degrés » de la trace de phase) montre une résonance à 14 MHz. Vous n’aurez peut-être pas besoin d’une valeur aussi élevée que 160 μH, mais vous aurez toujours l’avantage d’utiliser un bobinage constitué de peu de spires, donc avec peu d’effet capacitif entre spires. A utiliser en self de réjection en mode commun, mais déconseillé pour en faire une adaptation d’impédance ou un balun transformateur de tension
bobine D:
Ouille… avouez que ça fait peur. Encore une variété de Franken-bobine. Mais sommes-nous justes dans notre jugement ? Il s’agit d’une bobine qui date de plus de 50 ans, réalisée avec les meilleurs matériaux de l’époque : des torons de fils fins émaillés sous soie (fil de Litz) conçu pour fabriquer des bobinages d’antennes-cadre sur barreau de ferrite pour recevoir des ondes longues et moyennes. Cette série de mesures est donc légèrement sadique. Mais elle montre que tous les bobinages ne sont pas utilisables à n’importe quelle fréquence. Si vous souhaitiez réaliser une bobine comparable (180 μH) avec un noyau identique à celui de la bobine A, il vous faudrait recouvrir de fil toute la radio ellemême pour parvenir à cette valeur d’inductance. Et encore doit-on ajouter que cette valeur de 184 μH est atteinte sans le noyau de ferrite dont elle était accompagnée à l’origine. Son Q est de 26, ce qui n’est pas trop mal si on le compare à notre 4C65… mais passé 7 MHz, les jeux sont faits.
L’inductance fait un bon phénoménal vers les sommets puis s’enfonce dans les profondeurs. Le VNWA nous offre une fonction en prime : réglez le span (largeur de balayage) à 0, limite de fréquence de démarrage à 0,1 MHz, trace active « S11 LCR », et nous avons un superbe LRCmètre (cette mesure a été effectuée en utilisant la fameuse prise BNC sur laquelle était soudé directement le tore blanc 4C65, voir photo en début de chapitre)
Ainsi s’achève mon initiation au monde merveilleux des bobinages. Le contraire de l’inductance, c’est le condensateur. Le prochain chapitre va vous parler de ces petites bestioles que beaucoup considèrent comme des composants presqu’idéaux.
Le sont-ils ?
C’est ce que nous verrons
Fred PA4TIM
L’original de ce texte est disponible à l’adresse
http://www.pa4tim.nl/wp-content/uploads/2010/11/VNA_hfst2.pdf
L’intégralité du didacticiel est accessible à l’adresse
Le contenu de ce texte ne peut être modifié sans l’autorisation de son auteur. Traduction f6itu sous Creative Commons