Asservissement LQG drone quadrirotor

Présentation

Retour à User:Mael
La page suivante présente quelques travaux sur les méthodes d’asservissement modale et LQG d’un drone quadri rotor. Le principe détaillé ici est uniquement théorique, je n’ai pas réalisé de drone quadri rotor pour mettre en œuvre cette démarche. Cependant, j’ai mis en pratique ces équations pour la réalisation d’un drone hybride à voilure tournante Projets:Perso:2013:Drone hybride. Les algorithmes sont très similaires, avec juste une problématique supplémentaire dans le cas du drone hybride que j’aborderais plus loin. La démarche ainsi que les calculs sont issues de plusieurs livres très complémentaires sur le sujet :

Automatique \ Systèmes linéaires, non linéaires, à temps continus, à temps discret, représentation d'état \ Yves Granjon \ DUNOD : très intéressant pour des débutants en automatique, il repose bien toute la problématique en évoquant simplement la représentation d'état pour finir.
Commande et estimation multivariables \ Méthodes linéaires et optimisation quadratique \ Eric OSTERTAG \ Ellipses : dans la continuité du précédent, on entre cette fois dans le vif du sujet avec beaucoup d'explications et de démonstrations des formules utilisées ici. Il est nécessaire de connaitre assez bien l'automatique avant d'attaquer ce livre.
Automatique appliquée \ Philippe de Larminat \ Hermes Lavoisier : Pour les spécialistes, l'approche est plus ardue mais présente un panel complet de l'automatique tout en allant plus loin que les autres sur les aspects théorie et optimisations.
La commande multivariable \ Application au pilotage d'un avion \ Caroline Bérard - Jean-Marc Biannic - David Saussié \ DUNOD : Cas pratique mis en oeuvre, ce livre est sans doute le plus intéressant pour un ingénieur d'application, car il propose un axe pour la réalisation d'une étude de correcteur modale, LQG et H infini. Cependant, seul il n'est pas suffisant pour bien saisir toutes les subtilités et disposer de tous les outils nécessaires (notamment les observateurs).

En résumé, dans l'étude ci-dessous, il y a des choses piochées dans les 4 livres ci-dessus, principalement 4 pour la méthode et 2 pour les observateurs et intégrateurs, ainsi que le modèle discret. Cependant, étant moi-même ingénieur en automatique, je partais avec un certain background en automatique. Aussi je ne saurais trop conseiller à ceux qui souhaitent approfondir le domaine ou qui ne sont pas du sérail de se procurer les 4, même si j'admet que c'est un investissement certain... (environ 30 Euro chaque).

Modèle

Les données du modèle

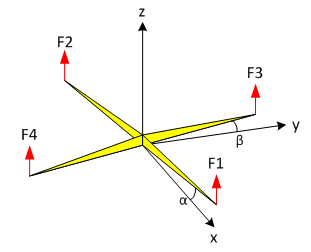
Le modèle retenu pour le drone quadri-rotor est le suivant :

Dans ce modèle, les paramètres F1, F2, F3 et F4 sont les efforts des actionneurs (moteurs électriques avec hélice) sur le drone (corps jaune) par rapport au sol. Les angles α et β sont respectivement les rotations de ce même corps par rapport à y et x.

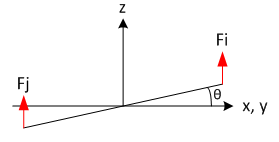
Deux sous-ensembles indépendants et génériques apparaissent dès lors que les angles α et β restent petits :

Dans le premier cas, on a :

$\theta=\alpha$ ,
$F_{{i}}=F_{{1}}$ ,
$F_{{j}}=F_{{2}}$ ,
Sur le plan (x,z)

Et dans le second cas :

$\theta=\beta$ ,
$F_{{i}}=F_{{3}}$ ,
$F_{{j}}=F_{{4}}$ ,
Sur le plan (x,z)

L’hypothèse des petits angles permet de négliger le couplage des angles l’un sur l’autre. Elle reste vraie tant que $Sin(\theta)\backsimeq\theta$ .

On pose également deux variables complémentaires dont l’utilité sera explicitée plus tard :

$\phi_{{1}}=F_{{1}}-F_{{2}}$
$\phi_{{2}}=F_{{3}}-F_{{4}}$

Les équations d'état

L’étude se positionne sur le modèle générique, sachant que la dynamique est la même pour $\alpha$ et $\beta$ . C’est d’ailleurs pour cette raison que les quadri-rotor en croix sont les plus simples à asservir.

Pour lier les efforts $F_{{i}}$ et $F_{{j}}$ des actionneurs à l’angle $\theta$ , on applique le principe fondamentale de la dynamique pour les rotations, à savoir :

${\color{Blue}J_{{y}}\cdot{\ddot{\theta}}=\overrightarrow{M}(F_{{i}})_{{i}}-% \overrightarrow{M}(F_{{j}})_{{j}}}$

Le Principe Fondamental de la Dynamique s’applique au centre de gravité, qui est également le centre géométrique du drone (point 0), on utilise alors la longueur du bras du drone (a) :

{\color{Blue}\overrightarrow{M}(F_{{i}})_{{i}}=\overrightarrow{OI}\wedge% \overrightarrow{F}_{{i}}+\overrightarrow{M}(F_{{i}})_{{O}}}

Sachant que le moment de

F_{{i}}

au point O est nul, on peut poser :

{\color{Blue}J_{{y}}\cdot{\ddot{\theta}}=a.F_{{i}}-a.F_{{j}}}

Et:

{\color{Blue}\phi_{{n}}=F_{{i}}-F_{{j}}}

D'ou :

{\color{Blue}J_{{y}}\cdot{\ddot{\theta}}=a.\phi_{{n}}}

On asservit sur

\theta

à partir de

\phi

car seul

\phi

peut être asservit par rapport

\theta

. En effet, si l’on conserve

F_{{i}}

et

F_{{j}}

, il existe une infinité de solution à l’équation (1.3). Quel que soit

F_{{i}}

, on peut trouver un

F_{{j}}

qui permette d’atteindre l’angle

\theta

de consigne. Ainsi, on utilise la variable

\phi

qui représente l’écart de poussée des deux actionneurs, qui est réellement la variable de contrôle de l’angle. Afin de prendre en compte un modèle proche de la réalité, on va utiliser un modèle du premier ordre pour représenter le moteur :

{\color{Blue}{\frac{F_{{i}}(p)}{U_{{i}}(p)}}={\frac{K_{{i}}}{1+\tau_{{i}}.p}}}

Dans ce modèle, K représente le gain de commande entre la commande (entre 0 et 300 pour cet exemple) et la poussée (en Newton) de chaque actionneur.

$\tau_{{i}}$ représente le retard de la commande. En effet, entre l'application de la commande et l’atteinte de cette commande par l'actionneur, il va se dérouler un certain temps associée à la dynamique du système.

Dans le cas où les actionneurs $F_{{i}}$ et $F_{{j}}$ sont identiques, avec la même dynamique, il est possible de considérer que la variable $\phi$ évolue dans les mêmes conditions, et de poser :

{\color{Blue}{\frac{\phi_{{n}}(p)}{U_{{n}}(p)}}={\frac{K_{{i,j}}}{1+\tau_{{i,j% }}.p}}}

Dans lequel $U_{{n}}$ est la différence entre les commandes $U_{{i}}$ et $U_{{j}}$ . La commande de chaque actionneur pourra être quelconque, la consigne sur $\theta$ sera atteinte dès lors que l’écart de commande $U_{{n}}$ entre $U_{{i}}$ et $U_{{j}}$ sera respecté.

On posera donc comme équations d'état les deux équations suivantes :

{\color{Blue}{\ddot{\theta}}={\frac{a}{J_{{y}}}}\times\phi_{{n}}}

{\color{Blue}{\dot{\phi}}_{{n}}=-{\frac{1}{\tau_{{i,j}}}}\times\phi_{{n}}+{% \frac{K_{{i,j}}}{\tau_{{i,j}}}}\times U_{{n}}}

Etude dans le domaine temporel

Modèle et retour d'état

La commande par retour d’état est une commande dans laquelle l’entrée du système est reliée à sa sortie par un paramètre fixe, appelé ici $K_{{c}}$ et en règle générale vectoriel ou matriciel, dont les valeurs sont associées à certaines caractéristiques attendues du système.

Avant de commencer, on pose le modèle sous sa forme d’état :

{\color{Blue}{\dot{X}}=A.X+B.U}

{\color{Blue}Y=C.X}

La variable X représente l’état du système, soit un ensemble de variables qui le caractérise dans le temps, et les matrice A, B et C les matrices du modèle qui le font évoluer dans le temps.

{\color{Blue}X={\begin{vmatrix}\alpha\\ {\dot{\alpha}}\\ \phi_{{1}}\\ \beta\\ {\dot{\beta}}\\ \phi_{{2}}\end{vmatrix}}}

La matrice A est composée deux deux blocs identiques, en

\alpha

et

\beta

, appelés

A_{{\alpha}}

et

A_{{\beta}}

:

{\color{Blue}A_{{\alpha/\beta}}={\begin{bmatrix}0&1&0\\ 0&0&{\frac{a}{J_{{y}}}}\\ 0&0&-{\frac{1}{\tau_{{n}}}}\end{bmatrix}}}

dans lequel n vaut 1 pour $\alpha$ et 2 pour $\beta$ . D'où :

${\color{Blue}A={\begin{bmatrix}A_{{\alpha}}&zeros(3,3)\\ zeros(3,3)&A_{{\beta}}\end{bmatrix}}}$

La matrice B assure le lien entre les consignes des actionneurs et l'état :

{\color{Blue}B={\begin{bmatrix}0&0\\ 0&0\\ {\frac{K_{{1}}}{\tau_{{1}}}}&0\\ 0&0\\ 0&0\\ 0&{\frac{K_{{2}}}{\tau_{{2}}}}\end{bmatrix}}}

Enfin, la matrice C filtre dans le vecteur d'état les variables accessibles en sorties, via les capteurs :

${\color{Blue}C={\begin{bmatrix}1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\end{bmatrix}}}$

Le vecteur de sortie Y est donc constitué des angles et vitesses angulaires autour des axes x et y.

On négligera d’entrée le lien direct entre la sortie et l’entrée, représenté par la matrice D. En règle générale il vaut mieux faire comme si on ne l'avait pas vu.

La commande modale

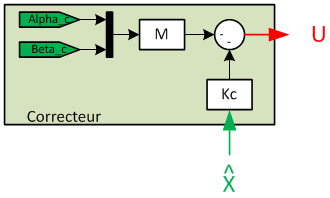
Le correcteur modal

Le correcteur modal est une matrice de gain qui permet, dans le modèle en boucle fermée suivant, de positionner les valeurs propres de la matrice d’état du modèle bouclé. En posant :

${\color{Blue}U=-K_{{c}}.X}$

On obtient le modèle en boucle fermée :

${\color{Blue}{\dot{X}}=(A-K_{{c}}.B).X}$

Dans ce modèle, le choix des valeurs propres de la matrice $(A-K_{{c}}.B)$ permet d’obtenir la convergence de l’état X vers son état stable :

Dans un temps minimum,
Avec un minimum de dépassement.

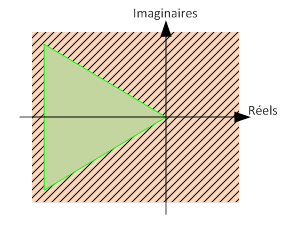
Le calcul de $K_{{c}}$ se base sur un vecteur propre dont les différentes valeurs sont associées aux variables de l’état. Les valeurs propres choisies, dans le cas temporel, doivent être négatives et à partie imaginaire dans la zone ci-dessous :

Les valeurs propres du système, choisies "judicieusement", permettent de caractériser le comportement du système. La zone ci-dessus est la zone optimale dans laquelle on obtient les meilleures performances pour le système. On pose le vecteur $V_{{c}}$ tel que :

${\color{Blue}V_{{c}}={\begin{bmatrix}\lambda_{{\alpha}}&\lambda_{{{\dot{\alpha% }}}}&\lambda_{{\phi_{{1}}}}&\lambda_{{\beta}}&\lambda_{{{\dot{\beta}}}}&% \lambda_{{\phi_{{2}}}}\end{bmatrix}}}$

Le calcul de la matrice de retour d'état Kc se fait, en utilisant Matlab, par la fonction :

${\color{Blue}K_{{c}}=place(A,B,V_{{c}})}$

Je ne rentrerais pas ici dans le détail de la fonction <place>. Elle sera étudiée plus tard pour les propriétés de découplage.

Le paramètre $K_{{c}}$ est utilisé uniquement pour asservir le modèle autour d'un point d'équilibre, ici en l’occurrence 0. Par défaut, le point d'équilibre est 0, sauf si une matrice de préfiltre, appelée M, permet d'intégré une constante dans le retour d'état, "décalant" l'asservissement vers un autre point d'équilibre et permettant ainsi de piloter le système. Je ne détaillerais pas ici le calcul de H puisque j'utiliserais la méthode des intégrateurs pour piloter le système et en profiter pour annuler l'erreur statique.

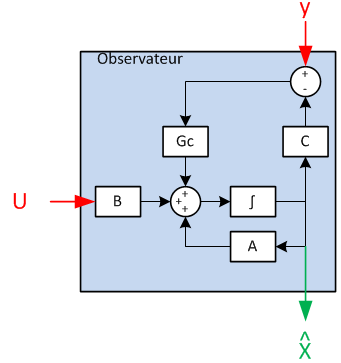
L'observateur modal

L’observateur est nécessaire car, même si les valeurs

\alpha,{\dot{\alpha}},\beta,{\dot{\beta}}

sont accessibles grâce à la centrale inertielle, il reste à estimer les variables

F_{{1}},F_{{2}},F_{{3}}

et

F_{{4}}

, c’est-à-dire

\phi_{{1}}

et

\phi_{{2}}

.

L’observateur assure le calcul de ${\hat{X}}$ , qui est une estimation de X. La commande sera basée sur ce ${\hat{X}}$ , et non sur le X qui est inaccessible en totalité.

L’observateur est alimenté par les sorties du modèles, c’est-à-dire les données issues de la centrale inertielle, et par la commande courante du modèle.

L’observateur est une image du modèle réel dont pour lequel on va pondérer l’influence de la boucle fermée, en utilisant une matrice G pour corriger l’état reconstruit à partir des valeurs accessibles. Un choix de valeurs propres du système corrigé par G permet de s’assurer que :

L’observateur converge vers le modèle réel,
La dynamique de convergence est plus rapide pour l’observateur que pour le modèle réel, sans quoi un retard de commande apparaitrait dans le système.

Le calcul de la matrice de gain de l’observateur se fait, par analogie avec la matrice du correcteur, par la fonction « place » de Matlab :

${\color{Blue}G_{{c}}=place(A^{\prime},C^{\prime},V_{{o}})^{\prime}}$

On utilise cependant la transposée de A au lieu de A, la transposée de C au lieu de B, et le vecteur propre $V_{{o}}$ des valeurs propres choisies pour l’observateur.

Les valeurs propres $V_{{o}}$ doivent être choisies à gauche (ie plus négative) :

${\color{Blue}\lambda_{{observateur}}<\lambda_{{correcteur}}}$

En moyenne, une valeur propre entre 1,2 et 2 fois inférieure est une bonne estimation pour démarrer.

L'intégrateur modale

Le système augmenté permet d’ajouter deux variables supplémentaires qui sont l’intégrale de α et β. Ces deux variables supplémentaires seront utilisées pour l’étage d’intégration assurant la correction de l’erreur statique.

{\color{Blue}{\dot{X}}_{{e}}=A_{{a}}.X_{{e}}+B_{{a}}.U}

{\color{Blue}Y=C_{{a}}.X_{{e}}}

Le système ainsi augmenté deviens :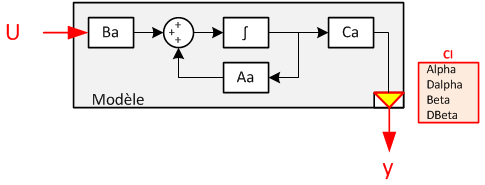

Les matrices A, B et C sont modifiées pour ajouter les paramètres d'intégration :

{\color{Blue}A_{{a}}={\begin{bmatrix}A&zeros(6,2)\\ -S_{{i}}.C&zeros(2,2)\end{bmatrix}}}

{\color{Blue}B_{{a}}={\begin{bmatrix}B\\ zeros(2,6)\end{bmatrix}}}

{\color{Blue}C_{{a}}={\begin{bmatrix}C&zeros(4,2)\end{bmatrix}}}

La matrice

S_{{i}}

permet de filtrer le vecteur Y pour en extraire

\alpha

et

\beta

, qui seront réinjectés dans l'étage d'intégration.

{\color{Blue}S_{{i}}={\begin{bmatrix}1&0&0&0\\ 0&0&1&0\end{bmatrix}}}

L'erreur statique entre les variables

\alpha

et

\beta

et leur consigne est intégrée, puis réintégrée à la commande U par une matrice de retour d'état

K_{{2}}

. Cette matrice de retour d'état est en réalité une sous-partie d'une matrice de correcteur

K_{{a}}

étendue, recalculée sur la base du modèle augmenté. Elle est calculée de manière similaire à la matrice

K_{{c}}

vue précédemment, à partir des matrices

A_{{a}}

et

B_{{a}}

, ainsi que d'un vecteur

\lambda_{{c}}

augmenté de deux valeurs propres, toujours négatives, pour les variables intégrales de

\alpha

et

\beta

. A titre d'exemple, les consignes suivantes sont appliquées au système (

\alpha_{{c}}

et

\beta_{{c}}

) :

Le modèle modale complet

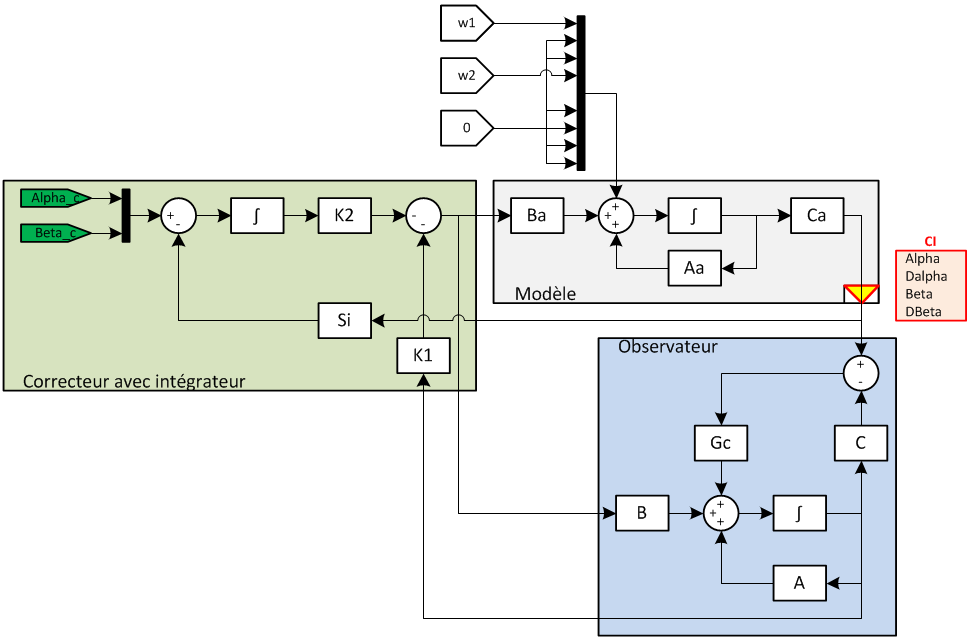
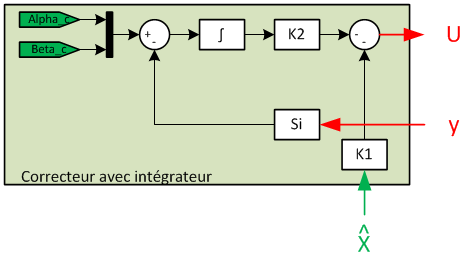
Le schéma ci-dessous résume les 3 étages du l'asservissement modale :

Le système augmenté,
L'observateur pour reconstruire l'état,
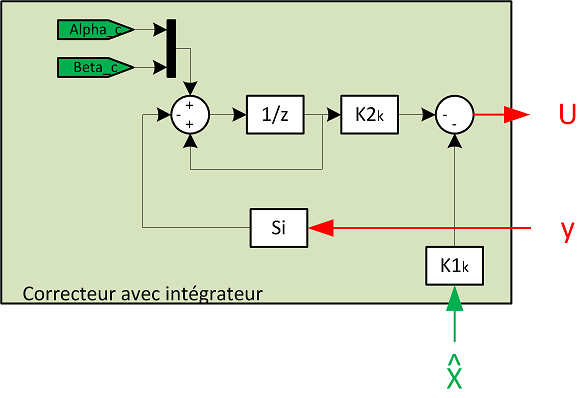
Le correcteur avec intégrateur.

Les paramètres w1 et w2 sont une représentation (pour l'instant symbolique) des perturbations sur le modèle. La modélisation nécessite de faire des hypothèses, qui engendrent nécessairement des erreurs de modélisation. Le système ne réagit pas exactement comme il est modélisé. A noter, on le verra plus tard, il y a aussi un bruitage à prendre en compte sur la sortie (sommé à Y).

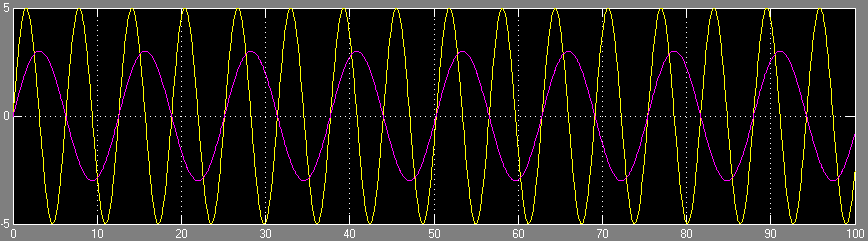
On obtient assez facilement, par placement de pôle (même si lui n'a rien de trivial et qu'il vaut mieux disposer d'un outils puissant pour le faire, comme Simulink) un asservissement avec de bons résultats :

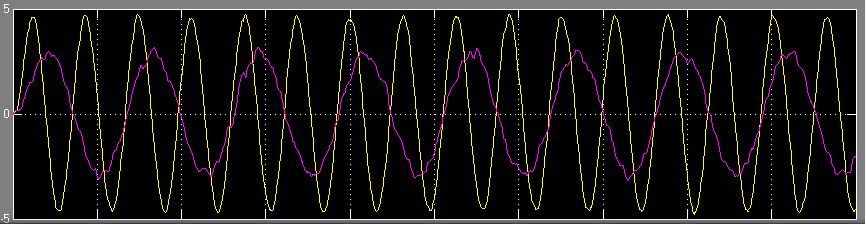
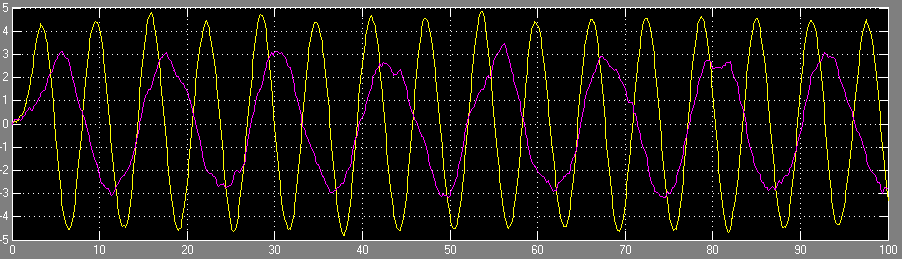
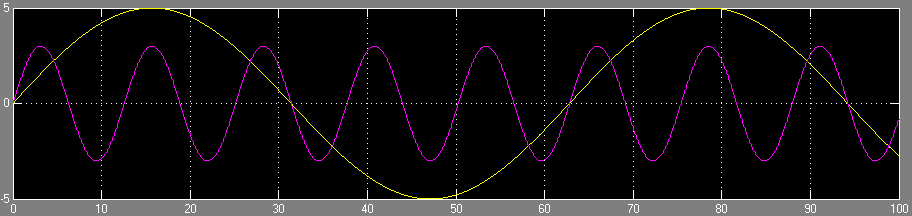
La sortie est présentée dans la figure ci-dessous :

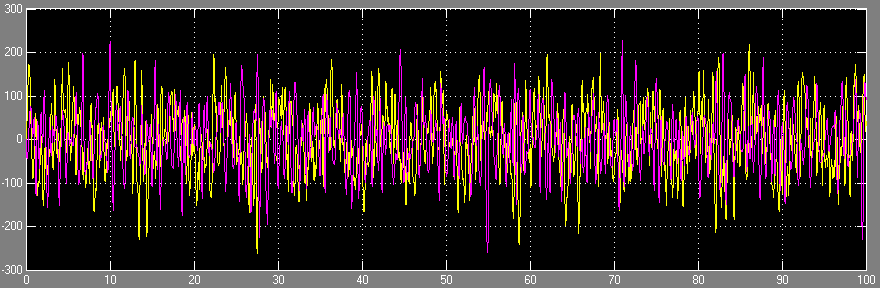
La commande des actionneurs est cependant beaucoup trop forte. En effet, pour corriger les bruits, le modèle va commander sur quasiment l'ensemble de sa gamme de commande, entre 0 et 300 :

Le problème de cette commande modale, c'est que l'on a fixé la dynamique du système avec le choix des valeurs propres de chacun des paramètres d'état, mais que cette dynamique engendre en général deux défauts majeurs :

Les consignes transmises aux actionneurs sont trop fortes,
Le système réagit beaucoup trop violemment à la moindre perturbation.

En l'état, elle ne sera pas utilisable.

Dernier point, et non des moindres, on ne pourra rien asservir avec un modèle en continu, il faudra passer sur du discret avec toutes les pertes de performances associées à un correction discrète (donc tous les dt secondes) au lieu d'une correction continue. Il reste du boulot...

Commande LQ

La commande LQ (Linéaire Quadratique) permet de pondérer les efforts d'asservissement entre l'amplitude des commandes et la dynamique du système. Dit autrement, il est possible d'agir sur le système asservit par deux moyens différents :

Augmenter la vitesse de réaction du système, c'est à dire qu'il atteindra sa consigne plus rapidement mais avec des consignes souvent irréaliste pour des systèmes physiques classiques,
Diminuer les consignes du système, afin de les rendre compatibles avec les capacités physiques des actionneurs, au détriment de la vitesse du système.

A noter, la synthèse modale d'un retour d'état va déjà permettre de fixer les dépassements et la vitesse globale du système, aussi va-t-on plutôt agir dans le sens d'une diminution des niveaux de consignes pour les rendre compatibles avec les actionneurs.

Initialisation du retour d'état

Le calcul d'une matrice de retour d'état de type LQ se base sur deux paramètres matriciels :

Matrice Q : matrice de pondération de la dynamique du système. Chaque paramètre dans la diagonale de cette matrice permet, s'il augmente, d'accroître la vitesse de convergence vers sa consigne du paramètre d'un vecteur d'état (i^ème ligne du vecteur d'état avec i^ème ligne de la matrice).
Matrice R : matrice de pondération de l'amplitude de la commande. Chaque paramètre dans la diagonale de cette matrice permet, s'il augmente, de diminuer l'amplitude de la commande associée dans le vecteur de commande (i^ème ligne du vecteur de commande avec i^ème ligne de la matrice).

Ainsi, la matrice Q est une matrice carrée de dimension n x n (n dimension du vecteur d'état) et R une matrice carrée de dimension p x p (p dimension du vecteur de commande). Q doit être définie positive (ie au moins un paramètre dans la diagonale différent de 0, et nécessairement positif) et R simplement positive (s'il y a des paramètres, ils sont positifs).

Dans la pratique, il revient à jouer les apprentis sorciers que d'essayer de trouver "à l'oeil" des paramètres pour Q et R qui donnent au système le comportement attendu. Il existe plusieurs méthodes pour y arriver (cf référence 3), j'en propose une issue du livre sur la commande multivariables (référence 4), qui consiste à repartir du correcteur modale et jouer ensuite sur le paramètre R pour limiter l'amplitude des commandes.

On va donc repartir du correcteur $K_{{a}}$ calculé pour le système augmenté, et créer les matrices Q et R à partir de là :

${\color{Blue}Q=(K_{{a}}^{\prime}.K_{{a}})}$

${\color{Blue}R=eye(p)}$

Le correcteur calculé à partir de ces deux matrices Q et R, donnera au système la même dynamique que dans le cadre du correcteur modale. On le constate d'après les équations : on positionne la pondération sur les variables d'état en fonction du correcteur $K_{{a}}$ , pour avoir une dynamique équivalente, mais on ne touche pas aux paramètres de commandes ("eye(n)" est un fonction Matlab construisant une matrice unité de dimension n x n, c'est à dire carrée avec des 0 partout sauf dans la diagonale ou l'on a que des 1).

Cependant, désormais il est possible de distinguer les pondérations "dynamique du système" des pondérations "commande". Il est donc plus facile de paramétrer le système.

Paramétrage du retour d'état

Le calcul du retour d'état sera basé sur les deux matrices de paramètres Q et R. On va donc modifier ces matrices initialisées précédemment pour paramétrer le système :

{\color{Blue}Q=Q+\delta Q}

{\color{Blue}R=R+\delta R}

La définition de

\delta Q

et

\delta R

est assez simple, elle permet de corriger les matrices initialisées en ajoutant dans la diagonale des paramètres beaucoup plus fort, accélérant le système ou limitant la commande. Ici on va plutôt mettre des paramètres très forts dans

\delta R

(>10000 dans mon appli) pour limiter l'amplitude des commandes.

Calcul du retour d'état LQ

Une fois les matrices Q et R initialisée et paramétrées, on calcule $K_{{lq}}$ le correcteur LQ associé à ces matrices.

{\color{Blue}[K_{{lq}},S,e]=lqr(A_{{a}},B_{{a}},Q,R,N)}

Je ne rentre pas dans le détail du calcul de $K_{{lq}}$ , il est très largement détaillé dans tous les livres traitant de la commande LQ (les références 2, 3 et 4 par exemple). Le calcul passe par la résolution de l'équation de Riccati, assez simple mais gourmand en temps, que la fonction $l q r$ de Matlab fait très bien. Les paramètres S et e ne sont pas utilisés (S : solution de l'équation de Riccati, pour les plus acharnés qui veulent vérifier, et e les valeurs propres de la boucle fermée, pour étudier leur décalage en fonction du paramétrage de Q et R). Le paramètre N est en général négligé dans la formule (ce que Matlab interprète par défaut comme N = 0).

La matrice $K_{{lq}}$ , comme $K_{{a}}$ , est découpée en deux parties :

$K_{{lq1}}$ : pour le vecteur ${\hat{X}}$ issu de l'observateur,
$K_{{lq2}}$ : pour le vecteur de commande issu de l'intégrateur.

Les correcteurs remplacent directement ceux du modèle modale, sans autres modifications.

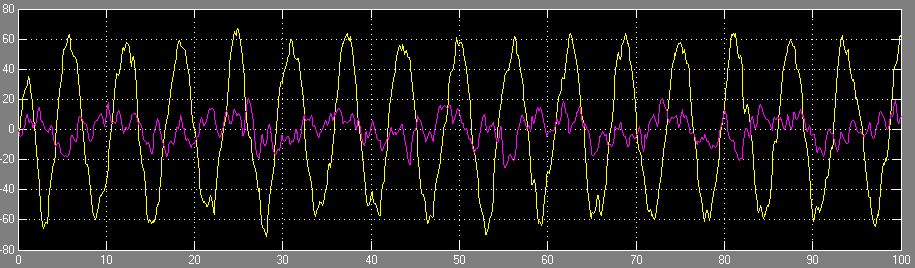
Les courbes ci-dessous présentent le résultat de l'asservissement du système soumis à deux consignes sur $\alpha$ et $\beta$ :

La consigne reste la même que pour la commande modale,
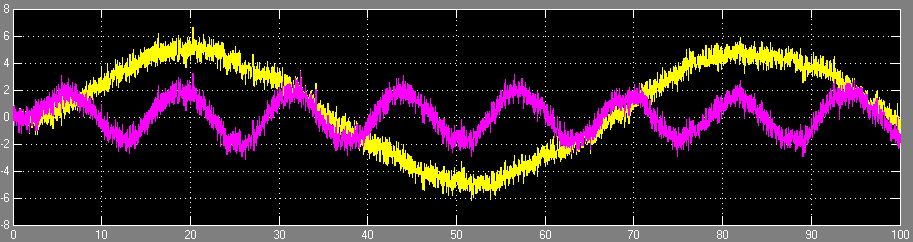
La sortie est présentée dans la figure ci-dessous, elle reste globalement similaire au cas modale :

La commande des actionneurs est limitée par rapport à celle de l'asservissement modale, mais elle reste assez forte. En réalité, elle est due à l'influence du bruit, qui sera filtré en discret par un filtre de Kalman :

Etude dans le domaine discret

Initialisation à partir du modèle temporel

L'initialisation à partir du modèle temporel est à privilégier lorsque ce modèle existe. Je ne reviens pas sur la théorie (ADU)

L'outil de discrétisation Matlab est la fonction :

systeme_discret = c2d(systeme_temporel,Te,'tustin')

Avec :

system_temporel créé avec la fonction ss(A, B, C),
systeme_discret créé à partir du système temporel,
Te période d'échantillonnage,
'tustin' méthode d'échantillonnage, nécessaire dès lors que l'on a un système avec des retards (typiquement le premier ordre des actionneurs).

Attention : sans la méthode "tustin", on obtient des amplitudes de commande hors norme.

D'après ce qui précède, dans l'étude temporel, il y a deux systèmes à discrétiser :

Système observé : celui utilisé par l'observateur, il s'agit des matrices A, B et C,
Système augmenté : incluant l'intégrateur, il est utilisé pour le calcul du correcteur.

Ainsi, on a :

system_obs_t = ss(A, B, C)
system_obs_k = c2d(system_obs_t, Te, 'tustin')
[Ak, Bk, Ck, Dk, dt] = ssdata(system_obs_k)

et :

system_aug_t = ss(Aa, Ba, Ca)
system_aug_k = c2d(system_aug_t, Te, 'tustin')
[Aak, Bak, Cak, Dak, dt] = ssdata(system_aug_k)

Da et Dak sont nuls, dt retrouve normalement la valeur de Te.

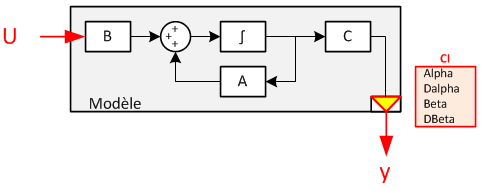
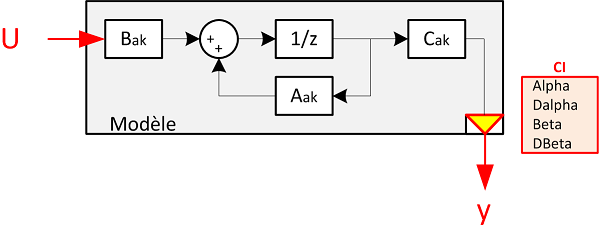
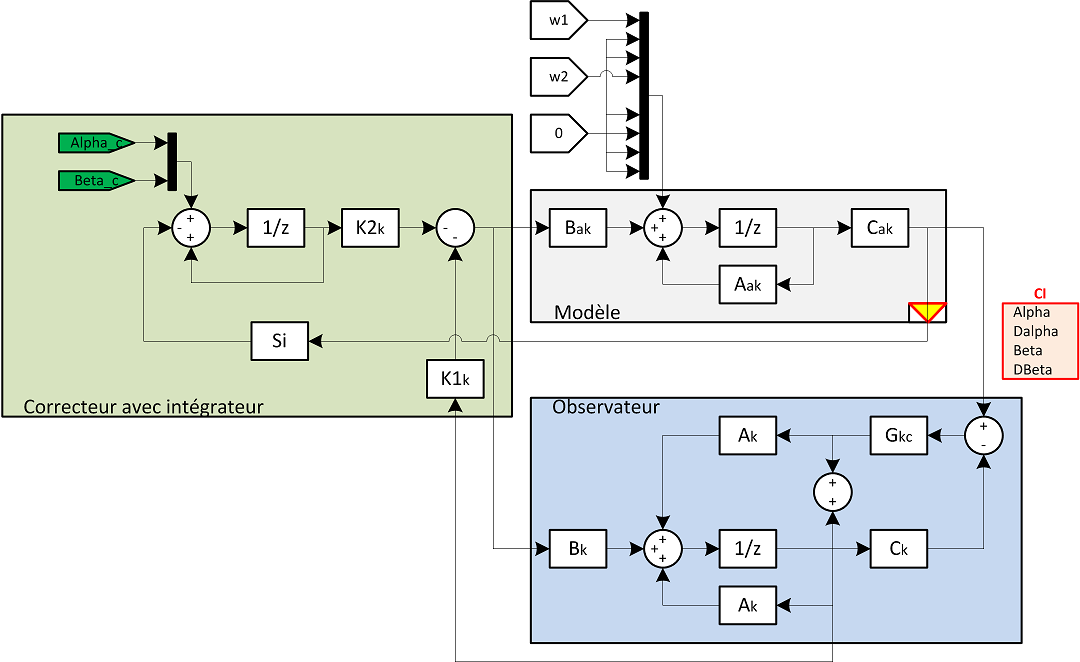
Le modèle discret étant créé, on va pouvoir reprendre une partie des calculs vus plus haut dans le domaine temporel pour le discret. Le schéma du modèle à asservir quand à lui est le suivant :

La seule différence avec le cas continu est l'utilisation d'un intégrateur discret (en

{\frac{1}{Z}}

) au lieu de l'intégrateur continu.

Choix des valeur propres discrètes (modale)

Les valeurs propres d'un système discret doivent être à l'intérieur du cercle unité pour que le système soit stable. A l'inverse du domaine temporel, ou la partie réelle de $\lambda_{{i}}<0$ , dans le domaine discret les valeurs absolues des parties réelles et imaginaires doivent être inférieures à 1 (elles-mêmes étant positives ou négatives).

Comme expliqué plus haut, il est intéressant de réaliser en premier lieu l'étude en temporel puis de discrétiser le système pour pouvoir utiliser le correcteur sur un équipement de contrôle commande (en général un microcontrôleur ou un PC, donc discret). Cependant, puisque l'on a trouvé des valeurs propres intéressantes en temporel, il serait bon de pouvoir les transformer elles aussi en discret.

On va ici utiliser une petite astuce perso, qui me semble logique (et qui a marché pour moi, donc..) :

Sachant que la discrétisation d'un modèle se fait par la fonction exponentiel,
L'exponentiel d'un nombre négatif est (oh magie!) inférieur à 1,

On réalise la discrétisation des valeur propres :

{\color{Blue}\lambda_{{i/k}}=\exp{\lambda_{{i}}}}

Alors certes ça ne marche pas parfaitement, mais c'est le résultat le plus probant que j'ai obtenu. A noter cependant, mais c'est assez normale, un asservissement dans le domaine discret à de moins bonnes performances que dans le domaine temporel (dépassement plus importants, amplitudes de commandes plus fortes, etc.). Par contre, plus la fréquence d'échantillonnage augmente, plus le modèle discret tend à recoller au modèle temporel. Donc si c'est tout moche après discrétisation, pas de panique ! Il faut juste posément reprendre les valeurs propres discrétisées et faire de nouveaux essais, même si, dans le cas d'un drone, une fréquence d'échantillonnage inférieure à 10 Hz aura rapidement de mauvaises performances quoi qu'il arrive.

Le correcteur modale discret

Celui-ci est facile à recalculer dès lors que l'on a les valeurs propres discrétisées et le système augmenté :

${\color{Blue}K_{{ak}}=place(A_{{ak}},B_{{ak}},[L1_{{k}}L2_{{k}}])}$

Note : $L1_{{k}}$ représente les valeurs propres pour le système standard, associées au vecteur $V_{{c}}$ , alors que $L2_{{k}}$ représente les valeurs propres discrètes de l'intégrateur.

On découpera à nouveau la matrice $K_{{ak}}$ en deux parties, une pour l'intégrateur et une pour le correcteur.

L'observateur modale discret

Je ne présente que succinctement l'observateur modale en discret, étant donné que l'on utilisera plutôt un filtre de Kalman (pour supprimer ou atténuer l'influence de w1 et w2, nettement plus concrète en discret).

L'observateur modale discret se calcul exactement comme dans le cas continu :

${\color{Blue}G_{{kc}}=place(A_{{k}}^{\prime},C_{{k}}^{\prime},V_{{ko}})^{% \prime}}$

Dans lequel $V_{{ko}}$ est directement issu de $L1_{{k}}$ , avec un coefficient k inférieur à 1 :

${\color{Blue}V_{{ko}}=k*L1_{{k}}}$

L'intégrateur discret

L'intégrateur discret est différent de l'intégrateur continu, essentiellement à cause de la discrétisation de l'intégrale. On a cette fois le schéma suivant :

La matrice Si est la même que dans le cas continu. Les consignes sont toujours appliquées au système via les deux entrées de commande $\alpha_{{c}}$ et $\beta_{{c}}$ . On utilise la consigne suivante dans la suite de cet étude :

Choix des matrices LQ discrètes

On reprend exactement la démarche du LQ continu :

Initialisation de ma matrice $Q_{{k}}$ à partir du correcteur modale : ${\color{Blue}Q_{{k}}=(K_{{ak}}^{\prime}.K_{{ak}})}$
Création d'une matrice $R_{{k}}$ identité : ${\color{Blue}R_{{k}}=eye(p)}$ , avec p actionneurs (2 dans notre cas)
Initialisation de la matrice $N_{{k}}$ : ${\color{Blue}N_{{k}}=-K_{{ak}}^{\prime}}$
Ajout d'un paramètre de réglage sur $Q_{{k}}$ : je rajoute la valeur 1 sur $\alpha$ et $\beta$ , tel que

${\color{Blue}\delta Q_{{k}}={\begin{vmatrix}1\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\end{vmatrix}}}$

sans oublier que l'on travaille à partir $K_{{ak}}$ et qu'il y a donc 8 paramètres à prendre en compte.

Ajout d'un paramètre de réglage sur $R_{{k}}$ : afin de bien ralentir le système, il ne faut pas hésiter à mettre de forts paramètres, tels que :

${\color{Blue}\delta R_{{k}}={\begin{vmatrix}10000\\ 10000\end{vmatrix}}}$

Mise a à jour des paramètres Q et R :

{\color{Blue}Q_{{k}}=Q_{{k}}+\delta Q_{{k}}}

{\color{Blue}R_{{k}}=R_{{k}}+\delta R_{{k}}}

Enfin, calcul du retour d'état $K_{{lqk}}$ par la fonction matlab dlqr (en non lqr comme dans le cas continu) :

{\color{Blue}[K_{{lqk}},S,e]=dlqr(Q_{{k}},R_{{k}},N_{{k}})}

On extrait ensuite :

${\color{Blue}K_{{lq1k}}=K_{{lqk}}(:,1:6)}$

${\color{Blue}K_{{lq2k}}=K_{{lqk}}(:,7:8)}$

qui sont en réalité les six première lignes de $K_{{lqk}}$ pour le correcteur basé sur ${\hat{X}}$ en sortie de l'observateur, et les deux paramètres qui restent correspondent à la partie intégrale.

Pour finir, on remplace $K_{{1k}}$ par $K_{{lq1k}}$ et $K_{{2k}}$ par $K_{{lq2k}}$ dans le schéma de l'intégrateur / correcteur pour avoir cette fois un retour d'état discret linéaire quadratique. Reste une dernière étape, le filtrage du bruit de mesure et du bruit de modèle pour éviter au système des réactions trop violentes dans les boucles d'asservissement. On utilisera pour cela un filtre de Kalman, bouclant ainsi notre commande LQG discrète.

Calcul du filtre de Kalman steady state

Il existe deux types de filtres de Kalman :

Le premier va évoluer dans le temps, en particulier la matrice de filtrage sera recalculée à chaque coup d'horloge. Ce filtre donnera les meilleurs résultats, car il est le plus dynamique, mais aussi beaucoup plus gourmand car il nécessite de lourd calculs à chaque coup d'horloge.
Le second est considéré à partir du moment où le système atteint un état stable, c'est à dire que l'on a quitté les états transitoires.

En première approche, je vais présenter ici un filtre steady state, c'est à dire à matrice de gain K invariante. Le second filtre sera présenté plus tard, mais internet fourmille d'études assez détaillées sur l'utilisation de ce type de filtres.

La première hypothèse du filtre de Kalman est d'avoir un bruit blanc, c'est à dire qu'il ne s'agit pas d'un biais défini masqué en bruit (auquel cas il faut ruser autrement).

Le calcul des paramètre du filtre de Kalman est assez similaire à celui du LQ, en utilisant deux matrices de pondération $W$ et $V$ . Ces matrices sont les matrices de covariances associées aux erreurs de modèle (liées à l'équation d'état) et de mesures (liées à l'équation de sortie).