Difference between revisions of "Asservissement LQG drone quadrirotor"

Revision as of 14:52, 20 April 2014 (view source) Mael (Talk | contribs) (→‎Position du modèle temporel) ← Older edit		Revision as of 14:54, 20 April 2014 (view source) Mael (Talk | contribs) (→‎Position du modèle temporel) Newer edit →
Line 141:		Line 141:
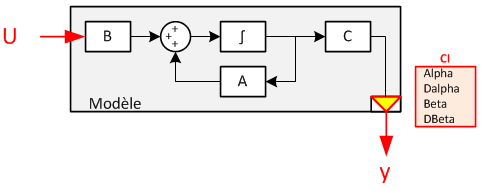
	On négligera d’entrée le lien direct entre la sortie et l’entrée, représenté par la matrice D. En règle générale il vaut mieux faire comme si on ne l'avait pas vu.		On négligera d’entrée le lien direct entre la sortie et l’entrée, représenté par la matrice D. En règle générale il vaut mieux faire comme si on ne l'avait pas vu.
		+
		+	[[File:systeme.png]]
	==== Le correcteur modal ====		==== Le correcteur modal ====

---

Revision as of 14:54, 20 April 2014

Présentation

Retour à User:Mael
La page suivante présente quelques travaux sur les méthodes d’asservissement modale et LQG d’un drone quadri rotor. Le principe détaillé ici est uniquement théorique, je n’ai pas réalisé de drone quadri rotor pour mettre en œuvre cette démarche. Cependant, j’ai mis en pratique ces équations pour la réalisation d’un drone hybride à voilure tournante Projets:Perso:2013:Drone hybride. Les algorithmes sont très similaires, avec juste une problématique dans le cas du drone hybride supplémentaire que j’aborderais plus loin.

Modèle

Les données du modèle

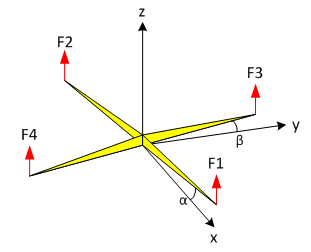
Le modèle retenu pour le drone quadri-rotor est le suivant :

Dans ce modèle, les variables F1 à F4 sont les efforts des actionneurs (moteurs électriques à hélice) sur le drone (corps jaune) par rapport au sol. Les angles α et β sont respectivement les rotations de ce même corps par rapport à y et x.

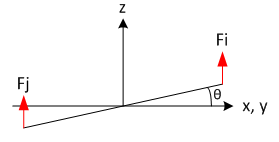
Deux sous-modèles indépendant apparaissent dès lors que les angles α et β restent petits :

Dans le premier cas, on a :

• $\theta =\alpha$,
• $F_i=F_1$,
• $F_j=F_2$,
• Sur le plan (x,z)

Et dans le second cas :

• $\theta =\beta$θ = β,
• $F_i=F_3$,
• $F_j=F_4$,
• Sur le plan (x,z)

L’hypothèse des petits angles permet de négliger le couplage des angles l’un sur l’autre. Elle reste vraie tant que $Cos(\theta )\theta$.

On pose également deux variables complémentaires dont l’utilité sera explicitée plus tard :

• ${\varphi }_1=F_1-F_2$
• ${\varphi }_2=F_3-F_4$

Les équations d'état

L’étude se positionne sur le modèle générique, sachant que la dynamique est la même pour $\alpha$ et $\beta$. C’est d’ailleurs pour cette raison que les quadri-rotor en croix sont les plus simples à asservir.

Pour lier les efforts $F_i$ et $F_j$ des actionneurs à l’angle $\theta$, on applique le principe fondamentale de la dynamique pour les rotations, à savoir :

$J_y\cdot \ddot{\theta }=\overrightarrow{M}{(F_i)}_i-\overrightarrow{M}{(F_j)}_j$

Le Principe Fondamental de la Dynamique s’applique au centre de gravité, qui est également le centre géométrique du drone (point 0), on utilise alors la longueur du bras du drone (a) :

$\overrightarrow{M}{(F_i)}_i=\overrightarrow{OI}\wedge {\overrightarrow{F}}_i+\overrightarrow{M}{(F_i)}_O$ Sachant que le moment de $F_i$ au point O est nul, on peut poser : $J_y\cdot \ddot{\theta }=a.F_i-a.F_j$ Et: ${\varphi }_n=F_i-F_j$ D'ou : $J_y\cdot \ddot{\theta }=a.{\varphi }_n$ On asservit sur $\theta$ à partir de $\varphi$ car seul $\varphi$ peut être asservit par rapport $\theta$. En effet, si l’on conserve $F_i$ et $F_j$, il existe une infinité de solution à l’équation (1.3). En effet quel que soit $F_i$, on peut trouver un $F_j$ qui permette d’atteindre l’angle $\theta$ de consigne. Ainsi, on utilise la variable $\varphi$ qui représente l’écart de poussée des deux actionneurs, qui est réellement la variable de contrôle de l’angle. Afin de prendre en compte un modèle proche de la réalité, on va utiliser un modèle du premier ordre pour représenter le moteur : $\frac{F_i(p)}{U_i(p)}=\frac{K_i}{1+{\tau }_i.p}$

Dans ce modèle, K représente le gain de commande entre la commande (entre 0 et 300 pour cet exemple) et la poussée (en Newton) de chaque actionneur.

$T_i$ représente le retard de la commande. En effet, entre le démarrage de la commande et l’atteinte de cette commande par la système, il va se dérouler un certain temps associée à la dynamique du système.

Dans le cas où les actionneurs $F_i$ et $F_j$ sont identiques, avec la même dynamique, il est possible de considérer que la variable $\theta$ évolue dans les mêmes conditions, et de poser :

$\frac{{\varphi }_n(p)}{U_n(p)}=\frac{K_{i,j}}{1+{\tau }_{i,j}.p}$

Dans lequel Un est la différence entre les commandes $U_i$ et $U_j$. La commande de chaque actionneur pourra être quelconque, la consigne sur $\theta$ sera atteinte dès lors que l’écart de commande $U_n$ sera respecté.

On posera donc comme équations d'état les deux équations suivantes :

$\ddot{\theta }=\frac{a}{J_y}\times {\varphi }_n$ ${\dot{\varphi }}_n=-\frac{1}{{\tau }_{i,j}}\times {\varphi }_n+\frac{K_{i,j}}{{\tau }_{i,j}}\times U_n$

Commande modale par retour d'état

Position du modèle temporel

La commande par retour d’état est une commande dans laquelle l’entrée du système est reliée à sa sortie par un paramètre fixe, appelé ici $K_c$ et en règle générale matriciel, dont les valeurs sont associées à certaines caractéristiques attendues du système.

Avant de commencer, on pose le modèle sous sa forme d’état :

$\dot{X}=A.X+B.U$ $Y=C.X$ La variable X représente l’état du système, soit un ensemble de variables qui le caractérise dans le temps, et les matrice A, B et C les matrices du modèle qui le font évoluer dans le temps. $X=\left|\begin{array}{c}\hfill \alpha \hfill \\ \hfill \dot{\alpha }\hfill \\ \hfill {\varphi }_1\hfill \\ \hfill \beta \hfill \\ \hfill \dot{\beta }\hfill \\ \hfill {\varphi }_2\hfill \end{array}\right|$ La matrice A est composée deux deux blocs identiques, en $\alpha$ et $\beta$, appelés $A_{\alpha }$ et $A_{\beta }$ :

dans lequel n vaut 1 pour $\alpha$ et 2 pour $\beta$. D'où :

La matrice B assure le lien entre les consignes des actionneurs et l'état :

Enfin, la matrice C filtre dans le vecteur d'état les variables accessibles en sorties, via les capteurs :

Le vecteur de sortie Y est donc constitué des positions et rotations angulaires autour des axes x et y.

On négligera d’entrée le lien direct entre la sortie et l’entrée, représenté par la matrice D. En règle générale il vaut mieux faire comme si on ne l'avait pas vu.

Le correcteur modal

Le correcteur modal est une matrice de gain qui permet, dans le modèle en boucle fermée suivant, de positionner les valeurs propres de la matrice d’état du modèle bouclé. En posant :

$U=-K_c.X$

On obtient le modèle en boucle fermée :

$\dot{X}=(A-K_c.B).X$

Dans ce modèle, le choix des valeurs propres de la matrice $(A-K_c.B)$ permet d’obtenir la convergence de l’état X vers son état stable :

• Dans un temps minimum,
• Avec un minimum de dépassement.

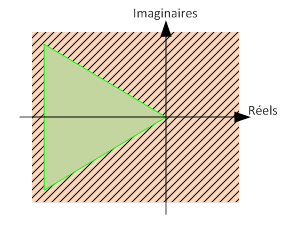
Le calcul de $K_c$ se base sur un vecteur propre dont les différentes valeurs sont associées aux variables de l’état. Les valeurs propres choisies, dans le cas temporel, doivent être négatives et à partie imaginaire dans la zone ci-dessous :

Les valeurs propres du système, choisies "judicieusement", permettent de caractériser le comportement du système. La zone ci-dessus est la zone optimale dans laquelle on obtient les meilleures performances pour le système. On pose le vecteur $V_c$ tel que :

Le calcul de la matrice de retour d'état Kc se fait, en utilisant Matlab, par la fonction :

$K_c=place(A,B,V_c)$

Je ne rentrerais pas ici dans le détail de la fonction <place>. Elle sera étudiée plus tard pour les propriétés de découplage.

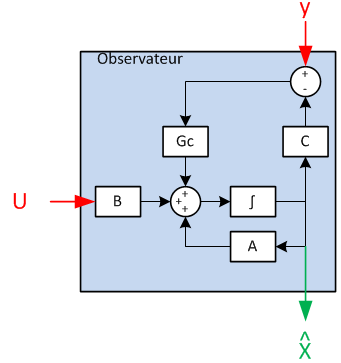
L'observateur modal

L’observateur est nécessaire car, même si les valeurs $\alpha ,\dot{\alpha },\beta ,\dot{\beta }$ sont accessibles grâce à la centrale inertielle, il reste à estimer les variables $F_a$ et $F_b$, c’est-à-dire ${\varphi }_1$ et ${\varphi }_2$.

L’observateur assure le calcul de $\widehat{X}$, qui est une estimation de X. La commande sera basée sur ce $\widehat{X}$, et non sur le X qui est inaccessible en totalité.

L’observateur est alimenté par les sorties du modèles, c’est-à-dire les données issues de la centrale inertielle, et par la commande courante du modèle.

L’observateur est une image du modèle réelle dont on va pondérer l’influence de la boucle fermé, en utilisant une matrice G pour corriger l’état reconstruit à partir des valeurs accessibles. Un choix de valeurs propres du système corrigé par G permet de s’assurer que :

• L’observateur converge vers le modèle réel,
• La dynamique de convergence est plus rapide pour l’observateur que pour le modèle réel, sans quoi un retard de commande apparaitrait dans le système.

Le calcul de la matrice de gain de l’observateur se fait, par analogie avec la matrice du correcteur, par la fonction « place » de Matlab :

$G_c=place{(A^{\prime },C^{\prime },V_c)}^{\prime }$

On utilise cependant la transposée de A au lieu de A, la transposée de C au lieu de B, et le vecteur propre $V_c$ des valeurs propres choisies pour l’observateur.

Les valeurs propres $V_c$ doivent être choisies à gauche (ie plus négative) :

En moyenne, une valeur propre 2 fois inférieure est une bonne estimation pour démarrer.

L'intégrateur modal

Le système augmenté permet d’ajouter deux variables supplémentaires qui sont l’intégrale de α et β. Ces deux variables supplémentaires seront utilisées pour l’étage d’intégration assurant la correction de l’erreur statique.

${\dot{X}}_e=A_a.X_e+B_a.U$ $Y=C_a.X_e$ $B_a=\left[\begin{array}{c}\hfill B\hfill \\ \hfill zeros(2,6)\hfill \end{array}\right]$