Difference between revisions of "Projets:Perso:2013:Module de localisation"
(→Calculs de Triangulation) |
(→Calculs de Triangulation) |
||
| Line 53: | Line 53: | ||
: Avec : Sin[Pi - θAB - a] = Sin[θAB] x Cos[a] + Sin[a] x Cos[θAB] | : Avec : Sin[Pi - θAB - a] = Sin[θAB] x Cos[a] + Sin[a] x Cos[θAB] | ||
D’où, tous calculs fait : | D’où, tous calculs fait : | ||
| + | {| class="wikitable centre" width="80%" | ||
| + | |+ Tableau | ||
| + | |- | ||
| + | ! scope=col | test | ||
| + | |- | ||
| + | |||
| + | |} | ||
Revision as of 23:48, 11 March 2014
Contents
Localisation par balisage infrarouge
Cette page présente mes travaux actuels sur la fabrication d'un système de balisage infrarouge pour mobile.
Le système contient les fonctions suivantes :
- Emission infrarouge de 4 balises autonomes,
- Réception infrarouge sur une tourelle,
- Contrôle d'un moteur pas à pas d'entrainement de la tourelle.
En plus de la fonction de triangulation associée au balisage, le système intègre en permanence deux entrées codeuses, assurant ainsi l'odométrie du mobile.
Les données d'odométrie sont ensuite intégrées aux données de balisage en permanence par l'intermédiaire d'un filtre de Kalman.
Un troisième volet de ce projet est le calcul en permanence d'une "void area", basée sur un réseau de capteurs ultrason déployés sur le mobile.
Dans un second temps, un autre projet viendra compléter celui-ci avec la réalisation d'un système de contrôle commande des moteurs (en DC, stepper DC puis en BLDC) avec un calcul de trajectoire basé sur les splines de Catmull-Rom.
Système de balisage infrarouge
Le principe de balisage infrarouge consiste à utiliser des balises émettant un signal infrarouge que va détecter un plot central, déployé sur une structure mobile roulante par exemple.
Le concept est développé dans le cadre de la coupe de France de robotique, et permet de disposer facilement d’une information de localisation sur la table de 3x2m.
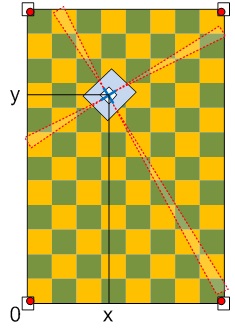
Le but est d’obtenir la meilleur estimation de x et y afin d’avoir la position du robot sur la table, ainsi que son orientation.
Le principe appliqué est celui de la triangulation, basée sur une mesure d’angle (il existe le même principe avec les distances, tout n’étant au final qu’une application des équations de trigonométrie).
Le choix du balisage infrarouge est lié au faible coût de la mise en œuvre (une centaine d’euros tout compris) et à la relativement grande précision du système.
Il sera couplé, dans la suite de ce document, à un dispositif d’odométrie et un dispositif de sonars permettant d’affiner la position courante du robot et de créer une « void area » autour du robot indiquant les zones accessibles ou non au robot.
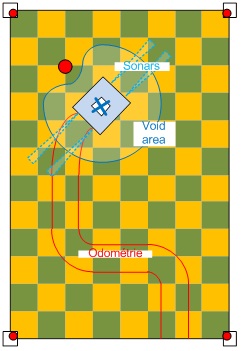
Les concepts définis par la suite s'appuient principalement sur deux éléments :
Le détail de l'utilisation de ces composants est donné dans les pages associées.
Balisage infrarouge
Le principe de la triangulation est de mesurer trois angles entre des points fixes et un point mobile, et de retrouver, connaissant la position des points fixes, la position du point mobile. La manœuvre est limité à la détection d’objets à l’intérieur de la zone formée par les points fixes (c’est peut-être possible en dehors, mais je n’ai pas fait l’analyse, pas besoin).
Le nombre limite de points fixes est au minimum de 3, dans le cadre de l’étude 4 seront utilisés (par extension de la version à 3 points). Plus il y a de points fixes, meilleure est la précision, mais plus long seront les traitements.
Calculs de Triangulation
Tout d’abord, définissons quelques variables. Le schéma ci-dessous représente la table sur laquelle est porté un repère orthonormé qui va servir de base aux calculs. Deux angles sont définis :
- θAB,
- θAC.
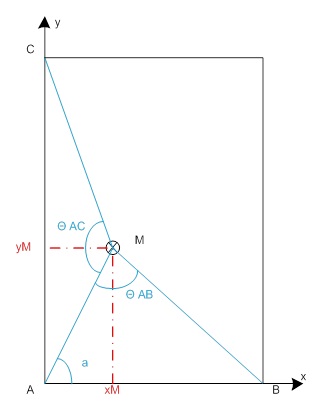 Le calcul de ces deux angles sera précisé plus bas. Pour l’instant, partons du principe qu’ils sont connus. Par triangulation, nous allons calculer xM et yM en calculant un certain nombre de variables de cette figure qui nous donnerons, in fine, les coordonnées du point M.
Le calcul de ces deux angles sera précisé plus bas. Pour l’instant, partons du principe qu’ils sont connus. Par triangulation, nous allons calculer xM et yM en calculant un certain nombre de variables de cette figure qui nous donnerons, in fine, les coordonnées du point M.
Par analyse du schéma, on pose :
- xM = AM x Cos[a]
- yM = AM x Sin[a]
Nota : pour ceux qui préfèrent travailler en polaire, il est possible d’utiliser AM (ie r) et a (ie θ) directement, par exemple pour trianguler la position d’un outil sur un bras SCARA.
Le calcul de la variable AM se base sur les trois formules suivantes :
- Loi des sinus : MB /Sin[a] = MA/Sin[Pi - θAB - a] = AB/Sin[θAB]
- Sin[Pi - x] = Sin[x]
- Sin[a+b] = Sin[a] x Cos[b] + Sin[b] x Cos[a]
On définit ainsi :
- MB = (AB x Sin[a]) / Sin[θAB] = (AM x Sin[a]) / Sin[Pi - θAB - a]
- Avec : Sin[Pi - θAB - a] = Sin[θAB] x Cos[a] + Sin[a] x Cos[θAB]
D’où, tous calculs fait :
| test |
|---|